作为防震减灾的重要手段,地震预警已经在全国范围内开始发挥减灾实效。国家地震烈度速报与预警工程项目(下文简称“预警工程”)中地震预警分系统实现了首台触发后数秒至数十秒的地震定位、实时的震级估算、预警目标区烈度计算及预警信息发布等功能,但实时计算大震断层破裂分布的功能尚未实现。现阶段,预警模块采用点源模型的烈度衰减关系预测大震烈度分布,对离震源较远但离断层很近地区的烈度预测明显偏小,可能造成这些震感强烈的地区没有发布预警信息。2011年东日本MW9.0地震期间,Kanto地区地震动被严重低估,没有发出预警信息(Böse et al,2012),便是一个典型的例子。
传统的大震断层反演大多根据远场地震数据和大地测量数据进行联合反演,通过多种条件约束,得到较为准确且稳定的破裂过程结果,一般在震后数小时才能产出地震破裂特征参数等信息(姚振兴等,1997;周仕勇等,2003、2006),传统的反演方法能够反演详细稳定的破裂过程,但大多耗时较长,难以满足地震预警对时效性的需求。
国际上已出现一些适用于地震预警的大震断层破裂反演方法,比较常见的有三种方法。一种是通过将大震断层分解成若干子断层,通过子断层波形包络的叠加,合成整个断层的展布(Cua,2005;Yamada et al,2008;康兰池,2010);第二种是通过破裂方向性函数确定断层的破裂方式和破裂方向(Boatwright,2007;Ben-Menahem,1961;Convertito et al,2012;冯继威,2019);最后一种是利用模板匹配技术,通过将台站实际观测值生成近断层区域的图像与模板库中的模板进行匹配,得到大震断层破裂的展布方向和长度的有限断层识别方法(FinDer)(Böse et al,2012、2018)。
上述三种方法,或是提取子断层波形包络合成整个断层包络,或是通过提前设定断层尺度,或是利用模板匹配技术,通过多次匹配得到断层的展布方向和破裂长度,但其有一个共同特点,即均是对主断层进行破裂方向和长度的计算,不能覆盖断层破裂造成的所有近场地震动强烈地区。Yamada等(2007)利用1979—2004年全球9个M6.5以上的大震,分别应用线性判别方法及贝叶斯理论得到能够将台站进行分类的判别函数,并应用到大震断层破裂区域的快速判别中。本文研究在Yamada等(2007)研究的基础上,直接对接收到的波形数据进行实时线性计算,满足地震预警系统实现快速实时反演断层破裂区域的需求,同时能够计算大地震造成的次生断层破裂区域分布范围,可以避免距主断层较远区域预警信息漏报的情况。由于场地条件等方面存在差异,本研究利用我国5个破坏性地震重新拟合出符合我国强震特征的线性判别函数,实现在地震预警系统中每秒钟模拟计算断层地表破裂面积。
1 研究数据我国强烈地震主要分布在四大地震带上,由于本研究使用的Fisher方法需要台站较好地包围断层,近断层处需要有一定数量的台站分布,考虑到震级和近断层台站分布两个因素,华北地震区重大地震强震记录较少,青藏高原地震区大震频发但台站分布不均导致靠近断层处强震台站数量较少,暂未选取以上两大地震频发区内的重大地震进行研究,最终本研究选取南北地震带及东南沿海地震带上发生的5个强震,利用加速度记录进行线性判别函数的提取(表 1)。
| 表 1 本研究所用地震 |
将全部台站按照距离断层模型(Ji et al,2003;Zhang et al,2008;王卫民等,2013;邓起东等,2007;王未来等,2014)的远近分为近源台站和远源台站两类。分类标准为:当台站距离断层的断层距大于10km时为远源台站,当断层距小于等于10km时为近源台站。按照此分类方式,本研究共计得到近源台站53个,远源台站630个,使用的断层模型和各个地震中台站的分类结果如 表 2所示。
| 表 2 台站分类结果 |
判别分析是根据总结出的样本数据规律对研究样本进行分类的一种方法。通过建立一个线性判别函数,利用已知组别的数据特征确定判别函数的系数,通过该判别函数可对研究样本进行组别判定,其关键是找到能将样本进行有效分类的指标(赵丽娜,2013),即分类特征值。线性判别函数的形式如下
| f=c1x1+c2x2+⋯+cnxn−d=cXi−d | (1) |
其中,Xi代表能够将样本有效分类的分类特征值,c代表分类特征值的系数,d代表判别边界常数,当cXi=d时,即为两个不同类别的分类边界。
地震波形提取的众多参数中,已有研究显示高频幅值随断层距增大而迅速衰减(Campbell,1981),本研究参考Yamada等(2007)的研究成果,采用垂直向峰值加速度(单位:gal)的对数和水平向合成峰值速度(单位:cm/s)的对数作为近源台站和远源台站的分类特征值,即式(1)中的Xi。为得到水平向速度记录,将EW向和SN向速度记录进行速度合成。
Fisher线性判别分析方法的核心思想是投影,即将高维空间中很难分开的样本投影到一维空间中可能区别明显。投影时要选择合适的投影方向,使投影后同一类别的样本尽量接近,不同类别的样本尽可能远离,可通过Fisher准则函数的极值,求取线性判别函数的系数。Fisher准则函数形式如下
| JF(w)=(˜u1−˜u2)2˜s21+˜s22=wTsbwwTsww | (2) |
其中,w为向量,
按照上述方法将5个地震全部台站记录的垂直向lgPGA、水平向lgPGV投影到一条直线上(图 1黑色直线),找到能将两类台站记录有效分类的投影方向(图 1绿线)。通过最佳投影方向求得线性判别函数的系数c1的值为9.84,c2的值为1.78,d的值选取5个地震中f0的最大值,最终取得的值为23.252。得到最终用于分类近源台站、远源台站记录的线性判别式如下
| f=9.84lgZa+1.78lgHv−23.252,{f>=0, 近源台站 f<0, 远源台站 | (3) |
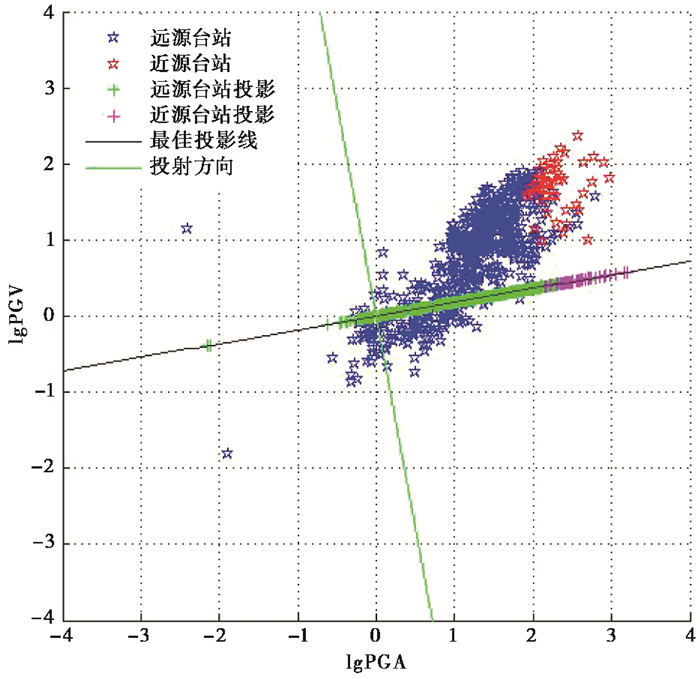
|
图 1 线性判别函数系数提取 |
其中,Hv代表水平向合成速度,Za代表垂直向加速度。
实际计算前断层位置未知,现有的台站分布不一定能满足计算需求,为了弥补因台站分布造成计算误差,利用liner线性插值方法,根据周围4个台站的f值直接插值得到待求插值点的f值,如 图 2所示,以待求插值点P为原点,四象限内分别距P点最近的A、B、C、D四个台站f值已知,首先在x方向上插值,得到R1、R2点f值,然后在y方向插值可得到P点f值,计算公式如下
| f(x,y)≈(x2−x)(y2−y)(x2−x1)(y2−y1)f(A)+(x2−x)(y−y1)(x2−x1)(y2−y1)f(B)+(x−x1)(y−y1)(x2−x1)(y2−y1)f(C)+(x−x1)(y2−y)(x2−x1)(y2−y1)f(D) | (4) |
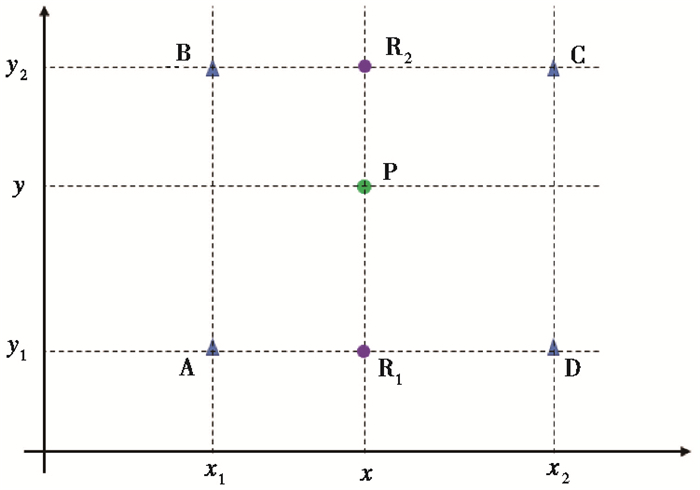
|
图 2 线性插值示意图 |
插值范围为台站分布的包络内,超出台站分布范围的地区不进行插值计算。
线性插值会造成插值点的地震动参数偏差,但该方法的主要目的是断层破裂区域的圈定,插值偏差相较整个断层破裂分布区域影响较小,且线性插值能够简化计算流程,每秒钟每个台站计算量更小,更加节省计算时间。汶川地震中插值间距为7.5km×7.8km(经度×纬度),共计插值1063个点。对113个台站进行线性判别函数值的实时计算,通过台站的f值插值得到1063个插值点的f值。
利用提取的线性判别函数(式(3))每秒钟计算一次各台站f值,利用f值进行台站性质判别及断层破裂区域圈定,步骤如 图 3所示。
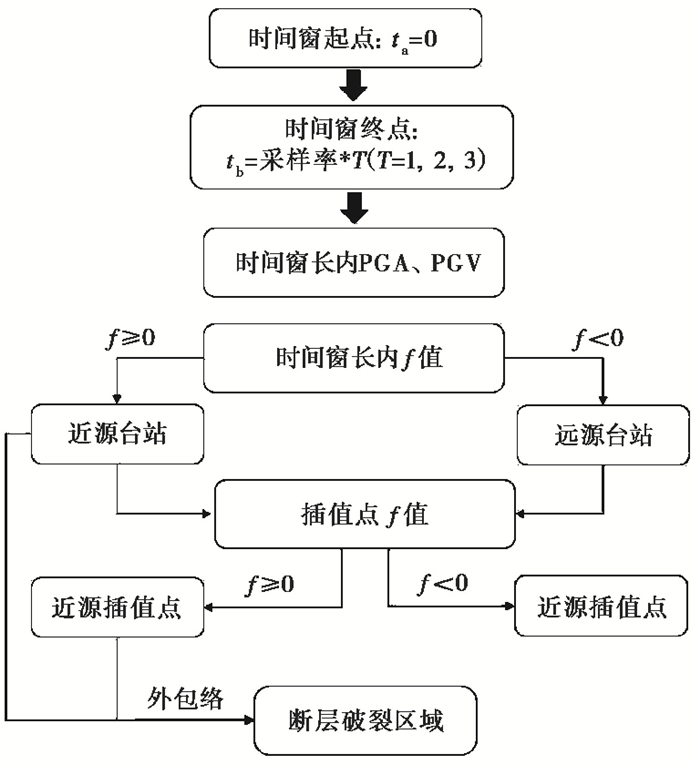
|
图 3 断层破裂区域计算流程 |
利用式(3)对强震断层破裂在地表的投影面积进行实时计算,限于篇幅,以2008年汶川8.0级地震为例,对计算过程进行详细分析。
据国家地震科学数据中心报道,此次地震震中位于四川汶川县映秀镇(103.42° E,31.01° N),震源深度14km,严重破坏面积超过100000km2。据中国地震局工程力学研究所的强震观测数据资料显示,汶川地震有效记录到地震信号的台站为113个(图 4),其中,距离汶川地震断层模型直线距离大于10km的台站有105个,断层距小于10km的台站有8个,台站分布虽局部较稀疏但能够包围断层位置,为本方法的应用提供了可靠的数据保障。
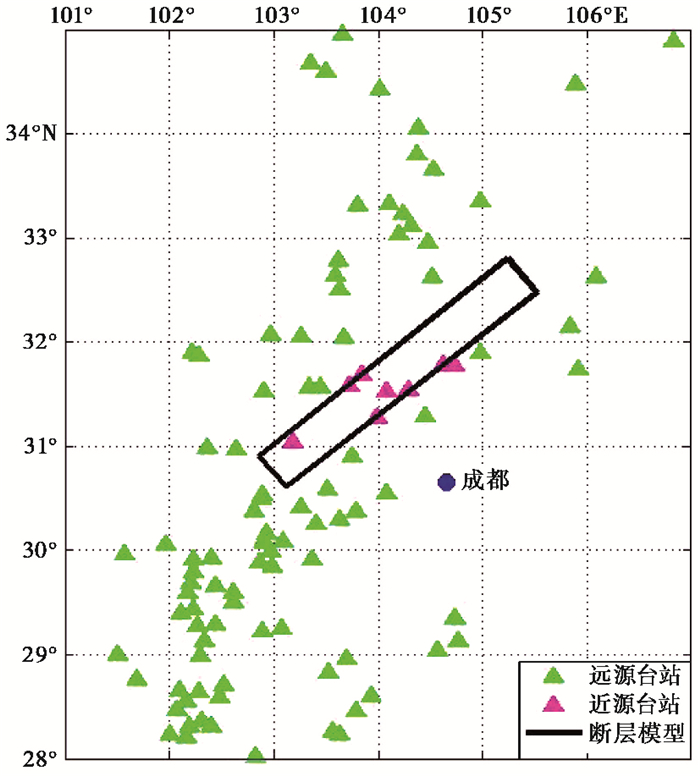
|
图 4 汶川地震台站分布 |
汶川地震中,强震台站授时不准确,利用P波理论到时与真实P波到时重叠,补齐或者删除台站噪声,对台站记录进行校正。利用校正后的记录进行模拟计算,震后5s判定第一个近源台站,根据近源台站和近源插值点的外包络线,得到实时断层破裂在地表投影面积,此时断层破裂在地表的投影面积为148km2。随着时间的推移,近源台站和近源插值点的数量不断增加,断层破裂在地表的投影尺度也逐渐增大。震后74s,计算结果稳定,不再随时间的推移而变化,最终反演断层破裂在地表的投影区域为51082km2。实时计算过程如 图 5所示,可以看出,距离震中较近的台站并不一定比距离震中较远的台站先显示,即台站距离震中的远近并不能决定其显示的先后,这也充分说明了距离震中的远近并不能决定其破坏程度,距离断层的远近才是决定其地震动参数大小的关键因素,图 5中不同颜色标度代表f值的大小,在一定程度上能够反映受灾程度的大小。
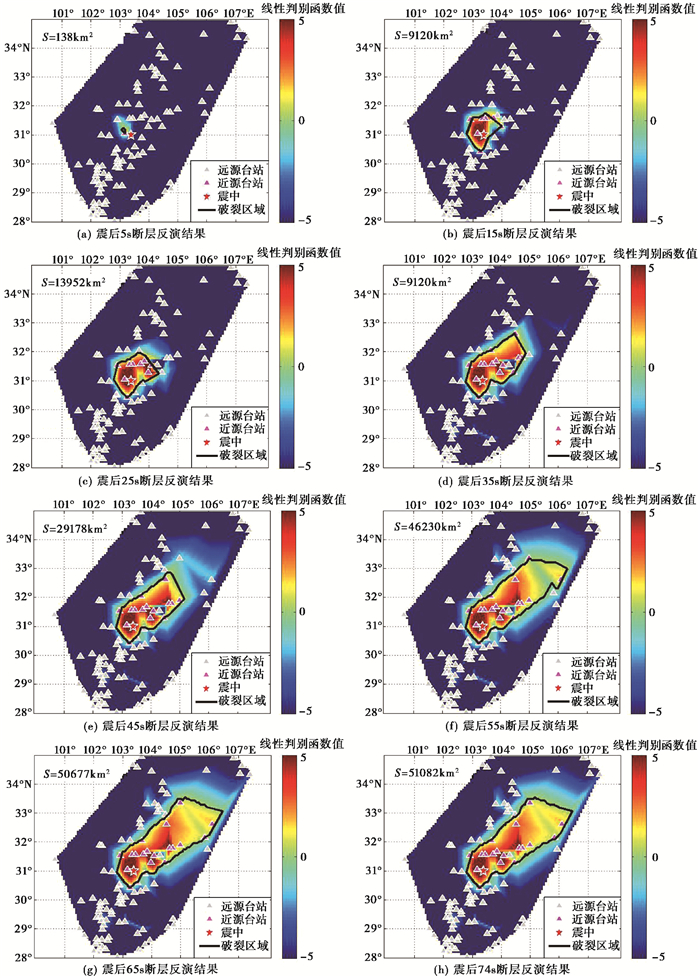
|
图 5 汶川地震地表破裂区域实时反演过程 |
汶川地震后,中国地震局科学考察队立即对地震产生的地表破裂带进行了系统的考察,野外考察表明,北川—映秀断裂和灌县—江油断裂同时发生地表破裂,北川—映秀地表破裂带是汶川地震的主体地表破裂带,地表破裂带整体走向N42°±5° E,长度约240±5km(徐锡伟等,2008)。如 图 6所示,利用本研究方法反演出断层破裂在地表的投影区域能够很好地包容野外地质调查结果且断层展布方向基本一致。
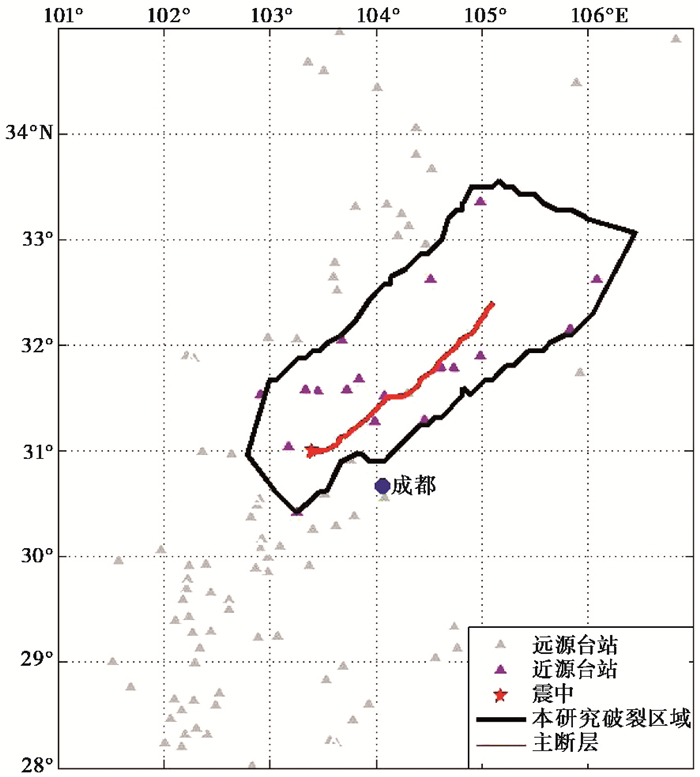
|
图 6 汶川地震研究结果与调查主断层结果对比 |
中国地震局专家据现场考察结果编制了汶川8.0级地震烈度分布图,此次地震断层呈NE向展布,Ⅺ度区以汶川和北川为两个中心呈长条状分布。本研究计算结果与Ⅷ度破坏区的展布方向一致,计算得到断层破裂面积为51082km2,Ⅷ度破坏区人工野外调查结果为27786km2,计算结果大于Ⅷ度区分布范围,如 图 7所示。汶川县、北川县、绵竹市、什邡市、青川县、茂县、安县、都江堰市、平武县、彭州市10个县市受灾极严重,均位于圈定的范围中。
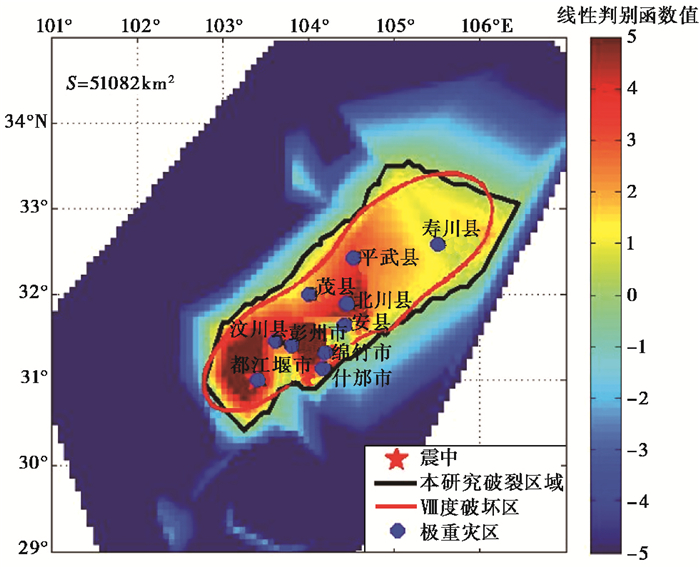
|
图 7 汶川地震反演结果与Ⅷ度区分布 |
集集地震断层破裂及其复杂,此次地震除了造成近SN向的主断裂活动外,在丰原东北部还有约15km的近EW向的断层破裂(王卫民等,2005)。选取我国台湾岛内的345个强震台站记录对此次地震进行研究,采样频率均为100Hz,计算结果如 图 8所示,反演结果基本能覆盖表 2中集集地震断层模型的分布范围,反演区域东南方向由于台站分布稀疏,反演结果与断层模型的分布有一定的差距。
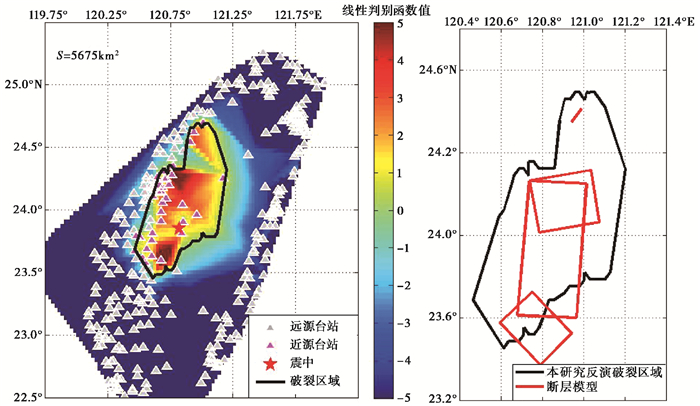
|
图 8 集集地震反演结果与断层模型分布对比 |
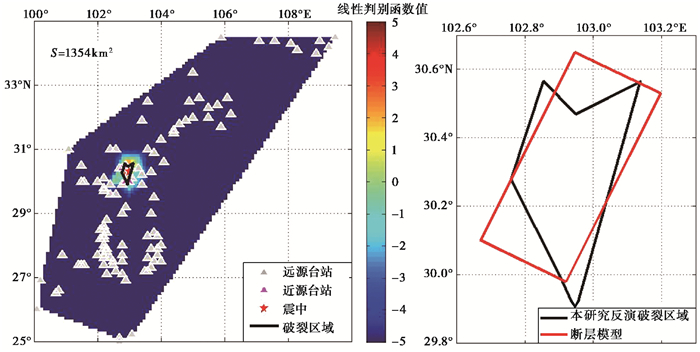
芦山地震反演结果仍具有一定的方向性,与断层模型方向基本一致,反演区域西南方向和东北方向由于台站较少,存在一定的偏差,反演结果如 图 9所示。
|
图 9 芦山地震反演结果与断层模型分布对比 |
鲁甸地震震级处于本研究判别函数适用范围的下限,反演结果已无明显的方向性,与点源模型相比已无明显优势,反演结果如 图 10所示。
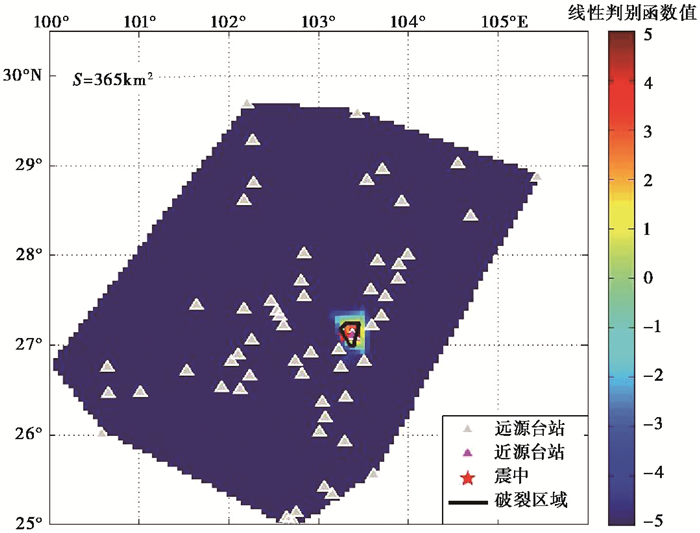
|
图 10 鲁甸地震反演结果 |
利用线性判别函数对5个强烈地震中近源台站记录的判别准确率达到90.57%,有5个近源台站记录判别错误,这会导致最终的判别区域面积减少,近源台站记录的判别效果将直接影响到最终结果的准确性(表 3)。
| 表 3 台站判别结果 |
利用本研究方法对上述5个大震断层进行模拟实时计算,在震后5s开始进行断层破裂区域的计算,一般在震后80s内得到稳定的计算结果,详细结果如 表 4所示。
| 表 4 计算时间及面积结果 |
汶川地震断层破裂是一个典型的单侧破裂,在本研究中,断层滑动前方高频幅值依然很大,计算出的结果明显较人工调查主断层结果偏大,断层滑动后方此现象不明显。在滑动前方,由于断层破裂速度和地震波在该方向上的传播发生了叠加,使得地震波形中的高频幅值叠加较断层滑动后方增大,由于多普勒效应的存在,断层滑动前方的计算边界比滑动后方的边界扩展大。
集集地震多条断层发生破裂,对于一次地震中多条断层发生破裂时,局部地区震动强烈并不是由主断层的破裂引发的,本研究方法通过对破裂区域进行圈定能更直观地说明地震动强烈地区的分布情况。由于中央山脉周围监测台站稀疏,导致最终的计算结果不能很好地包围断层,说明该方法的准确性有赖于高密度分布的台网。
利用线性判别方法对台站进行判别时,一般无需等到S波峰值到达便可完成台站性质的判别,有些强烈地震的P波波段便可以满足近源台站的判别,近源台站一般在地震动峰值达到之前便可以进行性质判别。
线性判别函数的系数应随仪器记录调整,目前我国已建成大量MEMS一般站,其观测记录与传统强震动台站记录存在差异,在使用这些数据前需对数据质量、噪声条件等进行检验。
5 结论利用我国5个典型强震加速度记录数据,提取出能够将台站性质进行分类的线性判别函数,并对汶川地震断层地表破裂区域进行模拟实时计算,实现在地震预警系统中每秒钟计算断层破裂区域在地表投影面积。结果表明,Fisher线性判别理论能够在地震预警允许的时间范围内得到网内地震合理的断层破裂分布范围。通过研究初步得出以下结论:
(1) 本研究对线性判别函数的提取依据我国5个典型的重大破坏性地震(M>6.5),经验证在台站包围震中效果较好的情况下,本研究拟合出的线性判别函数能够实时地对台站记录进行有效分类,对近源台站和远源台站的判别准确率均在90%以上。模拟计算结果基本能覆盖断层在地表的投影区域,即对于网内大震基本适用。对于6.5级以下地震的计算无明显方向性,网外地震及震级较小地震的适用性有待验证。
(2) Fisher线性判别方法能够在震后5~20s开始计算大震断层破裂在地表的投影面积,基本满足地震预警对时效性的需求,对于集集地震、汶川地震等特大地震,可在震后60~90s得到稳定结果,能够为地震预警第二报及后续处理过程提供服务。
(3) 本研究方法能够实时计算地震引发的多断层破裂区域,对于远离主断层但震动强烈地区可进行实时圈定,但该方法对台网密度要求较高,台站稀疏时,圈定区域边缘地区的计算准确性会降低。
邓起东、冉康勇、杨晓平等, 2007, 中国活动构造图(1:400万), 北京: 地震出版社.
|
冯继威. 2019. 大震地震动场的实时估计. 博士学位论文. 哈尔滨: 中国地震局工程力学研究所.
|
康兰池. 2010. 大震烈度速报系统的应用技术研究. 博士学位论文. 福州: 福州大学.
|
王未来、吴建平、房立华等, 2014, 2014年云南鲁甸MS6.5地震序列的双差定位, 地球物理学报, 57(9): 3042-3051. |
王卫民、赵连锋、李娟等, 2005, 1999年台湾集集地震震源破裂过程, 地球物理学报, 48(1): 132-147. |
王卫民、郝金来、姚振兴, 2013, 2013年4月20日四川芦山地震震源破裂过程反演初步结果, 地球物理学报, 56(4): 1412-1417. |
徐锡伟、闻学泽、叶建青等, 2008, 汶川MS8.0地震地表破裂带及其发震构造, 地震地质, 30(3): 597-629. |
姚振兴、纪晨, 1997, 时间域内有限地震断层的反演问题, 地球物理学报, 40(5): 691-701. |
赵丽娜. 2013. Fisher判别法的研究及应用. 硕士学位论文. 哈尔滨: 东北林业大学.
|
周仕勇、陈晓非, 2006, 近震源破裂过程反演研究——Ⅱ. 9.21中国台湾集集地震破裂过程的近场反演, 中国科学: (D辑), 36(1): 49-58. |
周仕勇、陈晓非、刘金朝等, 2003, 近震源破裂过程反演研究——Ⅰ, 方法和数字实验. 中国科学: (D辑), 33(5): 482-495. |
Ben-Menahem A, 1961, Radiation of seismic surface-waves from finite moving sources, Bull Seismol Soc Am, 51(3): 401-435. DOI:10.1785/BSSA0510030401 |
Boatwright J, 2007, The persistence of directivity in small earthquakes, Bull Seismol Soc Am, 97(6): 1850-1861. DOI:10.1785/0120050228 |
Böse M, Heaton T H, Hauksson E, 2012, Real-time Finite Fault Rupture Detector(FinDer)for large earthquakes, Geophys J Int, 191(2): 803-812. DOI:10.1111/j.1365-246X.2012.05657.x |
Böse M, Smith D E, Felizardo C, et al, 2018, FinDer v.2:improved real-time ground-motion predictions for M2-M9 with seismic finite-source characterization, Geophys J Int, 212(1): 725-742. DOI:10.1093/gji/ggx430 |
Campbell K W, 1981, Near-source attenuation of peak horizontal acceleration, Bull Seismol Soc Am, 71(6): 2039-2070. |
Convertito V, Caccavale M, De Matteis R, et al, 2012, Fault extent estimation for near-real-time ground-shaking map computation purposes, Bull Seismol Soc Am, 102(2): 661-679. DOI:10.1785/0120100306 |
Cua G B. 2005. Creating the virtual seismologist: developments in ground motion characterization and seismic early warning. Ph. D. thesis. Pasadena: California Institute of Technology.
|
Ji C, Helmberger D V, Wald D J, et al, 2003, Slip history and dynamic implications of the 1999 Chi-Chi, Taiwan, earthquake, J Geophys Res: Solid Earth, 108(B9): 2412. |
Yamada M, Heaton T, 2008, Real-time estimation of fault rupture extent using envelopes of acceleration, Bull Seismol Soc Am, 98(2): 607-619. DOI:10.1785/0120060218 |
Yamada M, Heaton T, Beck J, 2007, Real-time estimation of fault rupture extent using near-source versus far-source classification, Bull Seismol Soc Am, 97(6): 1890-1910. DOI:10.1785/0120060243 |
Zhang W, Shen Y, Chen X F, 2008, Numerical simulation of strong ground motion for the MS8.0 Wenchuan earthquake of 12 May 2008, Sci China Ser D: Earth Sci, 51(12): 1673-1682. DOI:10.1007/s11430-008-0130-4 |
 2024, Vol. 40
2024, Vol. 40



