体应变仪的观测原理最早是由Benioff(1935)提出,之后便由此发展出了Sacks-Evertson(Sacks et al,1971)、TJ(苏恺之等,1993)和小田原(Yoshikawa et al,2001)等型号的钻孔体应变仪。相比于地震仪、GNSS和InSAR等,该类仪器具有频带甚宽(零至数十赫兹)和分辨率高(优于10-10)等独特优势。在数十年的观测实践中,钻孔体应变仪已成为探索震源物理(Borcherdt et al,1989)、地震前兆(Linde et al,1988)、慢地震(Sacks et al,1982)和火山活动(Voight et al,2010)等地球动力学过程的重要工具。
但在日常观测中,气象(Nakao et al,1989;Canitano et al,2014;杨小林等,2021a)、Lamb波(吕品姬等,2022)、水文(吉田明夫等,1984)和钻孔应力状态(Yoshikawa et al,1992)等多重因素会对钻孔体应变仪产生明显干扰,而一些扰动的形态还与慢地震、前驱波和孤立波等相似。例如,Liu等(2009)在对中国台湾东部的钻孔体应变台进行分析时,就因忽视了台风过境时的降雨干扰,而误将一些瞬时应变事件推定为慢地震(Hsu et al,2015);再如,杨小林等(2021b)对华东地区钻孔体应变中形似孤立波或前驱波的信号进行了系统诊断,发现这些异常变化主要源于飑线。因此,如何阐明干扰噪声的物理源,一直是地壳形变观测和解释中的一大难点。
从气候背景来看,中国属于典型的季风气候区,在西伯利亚高压的作用下,寒潮天气较为频发(朱姜韬等,2022)。而所谓寒潮通常是指:某一地区冷空气过境后,气温24h内下降8℃以上,且最低气温下降到4℃以下;或48h内气温下降10℃以上,且最低气温下降到4℃以下;或72h内气温连续下降12℃以上,且最低气温在4℃以下。满足上述条件之一就可以判定为一次寒潮。这种灾害天气不仅影响范围大,而且还能造成霜冻和冻雨等自然灾害,常常会给社会、经济、生态和交通等带来严重影响。那么,寒潮对钻孔体应变台(网)的影响形态和机制究竟如何?截至目前尚缺乏针对性和系统性的研究。
2022年11月27日—12月1日,一次寒潮天气过程影响了整个江苏地区(Wang et al,2023;顾荣直等,2024),该事件导致区内5个钻孔体应变台出现了“迁移性”的群体响应,这为洞察寒潮干扰提供了较典型的个例,其例证价值较高。鉴于此,本文尝试对该寒潮所引致的钻孔体应变进行形态学和动力学诊断,相关结果将有助于此类干扰的人工或机器识别。
1 寒潮天气实况此次寒潮天气始于2022年11月27日中午,其传播路径自北向南推进(图 1),生命史则长达5天,导致江苏省内出现了剧烈的降温和大风等天气,其中南京市的降温幅度达17.57℃(Wang et al,2023;顾荣直等,2024)。该寒潮产生的天气动力学背景和具体的演化历程,可参照Wang等(2023)和顾荣直等(2024)的研究,此处不再赘述。总体来讲,此次寒潮事件具有降温幅度大和气压涌升量高等特点。
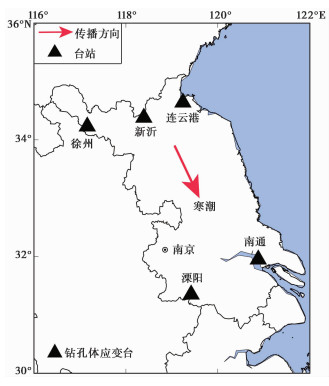
|
图 1 2022年11月27日—12月1日寒潮天气在江苏省的传播方向及钻孔体应变台分布 |
目前,江苏省共有15个TJ-2型钻孔体应变台,其辅助测项有室外气温、室外气压和钻孔水位,各测项的采样间隔均为1min。虽然此次寒潮影响了江苏省全境,但考虑到一些台站存在仪器故障和低信噪比等问题,故本文仅选取徐州、新沂、连云港、南通和溧阳这5个台站的观测数据。台站高程、钻孔应变仪探头埋深、钻孔围岩岩性等情况见 表 1。
| 表 1 台站高程、探头埋深及钻孔概况 |
为展示寒潮期间各台气温、气压和钻孔体应变的变化全貌,截取了2022年11月25日—12月6日期间各台分钟级的观测数据,详细结果如 图 2所示。从 图 2(a)、2(b)可以看到,在寒潮自北向南过境江苏期间,各台相继出现了显著的气温骤降和气压涌升现象(11月27日—12月1日);与此同时,钻孔体应变也发生了大幅的压应变变化(图 2(c))。
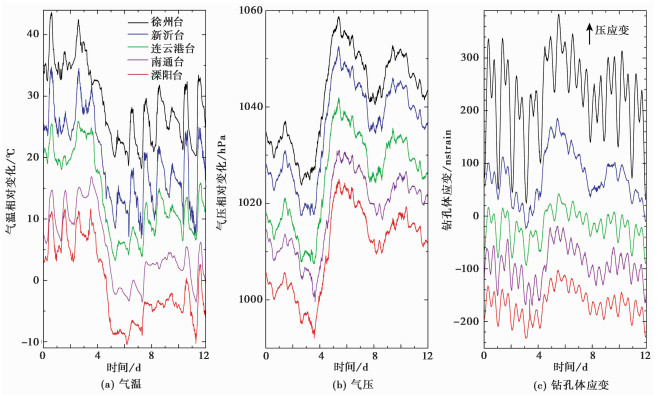
|
图 2 2022年11月25日—12月6日各台测项的变化实况 |
仔细观察 图 2可以发现,各曲线均叠加有高频和潮汐(日波、半日波和三分之一波等)信号;此外,寒潮干扰形态具有较强的非线性和非平稳特征。而这些因素对寒潮干扰的定量提取尤为不利。为此,本文采用经验模态分解(EMD)对原始观测数据进行预处理(Huang et al,2008),该步骤旨在剔除与寒潮无关的信号。以徐州台的气温测值为例,经EMD处理后,其时变曲线可分解为9个本征模态函数(IMF)和1项残差(Residual)(图 3)。进一步对比各IMF,便能明确寒潮导致的气温突降信号主要集中在IMF7~9,之后再对其进行叠加就能提取较合理的寒潮影响信号。限于篇幅,其他各测项的处理细节不再逐一描述,最终结果如 图 4所示。
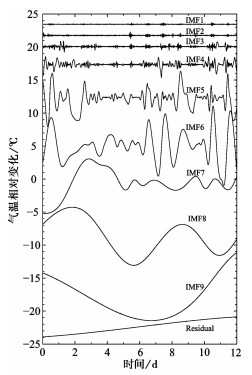
|
图 3 2022年11月25日—12月6日徐州台气温的EMD分解结果 |
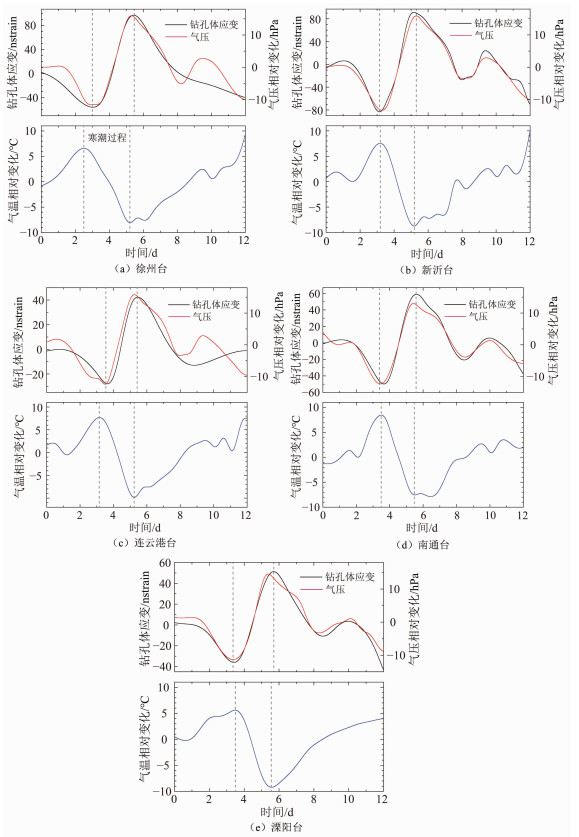
|
图 4 2022年11月25日—12月6日寒潮天气过程中各台钻孔体应变、气压和气温的响应变化 |
根据寒潮的演变历程,本文将气温大幅下降的时段定义为寒潮主时段,即 图 4中2条灰色虚线所界定的时段。与之相比,气压和钻孔体应变的响应时段则稍有差异。但从总体来看,各台具有以下几点共性特征:①气温在寒潮过程中呈大幅下降的走势;②气压与气温负相关,即展现为快速上升;③钻孔体应变与气压高度正相关。在此基础上,逐一统计各物理参量的变幅和持时等,具体结果列于 表 2。
| 表 2 各台不同测项对寒潮的响应量 |
从表 2不难发现,各台气温、气压和钻孔体应变对寒潮的响应量存有差异。对比来看,可归纳出如下几方面特点:①连云港台气温的降幅最大,为17.51℃,而徐州台的气温降幅最小,为14.66℃;②气压升幅最小和最大的台站分别为南通台和新沂台,其值依次为25.33hPa、29.23hPa;③连云港台的钻孔体应变响应量最小,为70.28 nstrain(nstrain=10-9),而新沂台最大,为174.57nstrain;④钻孔体应变的持时在2612~3454min之间;⑤气压系数介于2.49~5.97 nstrain/hPa之间。以上响应的个性特征,一方面说明了寒潮动力学过程的复杂性,另一方面也在一定程度上表征了各台台基介质的差异性。
4 钻孔体应变对寒潮响应的机制前文主要对钻孔体应变的响应特征及量值等进行了刻画,其响应机制无疑是一个值得深入探究的问题。首先,从时间域的相关性来看,寒潮期间的钻孔体应变与气温、气压分别具有负相关和正相关的关系(图 4)。但相关关系并不一定意味着因果关联。从物理机制上讲,由于气温在岩体中的热传导很慢,所以在数小时内,气温突变很难使地下数十米深的岩层出现热应变变形;而气压负荷却截然不同,其可以迫使近地表介质产生较即时的线弹性响应(Tsai et al,2004;Yang et al,2021;吕品姬等,2022),这也有效地解释了 图 4中气压与钻孔体应变形态相似的物理成因。
而另一个疑问便是,寒潮期间气压骤升所产生的理论钻孔体应变是否与观测值一致?对于周期性较强的气压负荷而言,其产生的理论钻孔体应变可根据张凌空等(2019)给出的解析公式进行定量计算。但考虑到气压骤升的非周期性,本文将问题作了简化处理,并假定钻孔所在地层为各向同性的弹性介质。依据胡克定律,在单轴应力作用时,理论钻孔体应变的解析解为(Hsu et al,2015)
| εv=(1−2ν)PE | (1) |
式中,εv为体应变,ν和E分别为钻孔围岩的泊松比和弹性模量,P为气压负荷。根据何斌等(2020)对江苏地区钻孔岩心的单轴压缩实验结果,灰岩、砂岩、片麻岩和安山岩的弹性模量值可依次取为32.4GPa、29.58GPa、38.8GPa和29.9GPa,泊松比则可取典型值0.25。再参照 表 2中各台气压的骤升量,徐州台、新沂台、连云港台、南通台和溧阳台所对应的理论钻孔体应变量分别为42.47 nstrain、49.41 nstrain、36.38 nstrain、42.82 nstrain和43.23 nstrain。将其与实测值进行对比,可以发现后者是前者的1.9~3.6倍(图 5)。之所以出现如此大的偏差,可能主要是由于实际地层的等效弹性模量值要远小于钻孔应变仪探头所在围岩处的测值。

|
图 5 理论与实测钻孔体应变响应量对比 |
在钻孔体应变对气压响应的时滞方面,徐州台、连云港台、南通台和溧阳台以滞后为主,滞后时长在52~306min以内。新沂台则出现了明显的超前现象,超前量为92min(图 4(b))。而之所以会出现超前响应,可能是由以下两方面因素所致:①钻孔体应变仪和气压计存在钟差问题(佟国刚等,2005;杨小林等,2023);②水平气压梯度力会导致区域地壳变形不同步(Kroner et al,2005;Yang et al,2021)。
综上分析,可以看出寒潮期间的气压骤升是钻孔体应变出现大幅压性变化的主因。
5 结论和讨论本文以2022年11月27日—12月1日发生在江苏省的寒潮事件为例,系统诊断了徐州台、新沂台、连云港台、南通台和溧阳台等5个钻孔体应变台对寒潮天气过程响应的特征与机制,主要结论如下:
(1) 寒潮可以使较大区域内的气温和气压产生迁移性的骤降和涌升变化,其最大变幅分别为17.51℃、29.23hPa。
(2) 在气压涌升的影响下,各台钻孔体应变大致以线弹性变形的方式响应气压变化,其持时在2612~3454min之间,最大变幅为174.57 nstrain,形态则与气压高度相关。从地面气象要素观测的视角来看,钻孔体应变仪亦可视为气压计。
(3) 徐州台、连云港台、南通台和溧阳台钻孔体应变对非周期气压的响应存在滞后现象,滞后时长在52~306min以内;新沂台则超前响应气压,超前量为92min。
(4) 气压负荷所引起的实测钻孔体应变量要远大于理论计算值,其原因可能是区域地层的等效弹性模量要低于钻孔应变仪探头处的围岩测值。
虽然本工作率先揭示了寒潮对钻孔体应变的影响形态和机制,但所获认识仍不全面,今后还需要对更多的寒潮干扰实例进行诊断。此外,钻孔体应变台的台基岩石(体)力学参数(如:弹性模量和泊松比等)和井孔耦合系数等,对理论气压负荷计算至关重要;因此,今后还需要进一步加强台基地层的岩石(体)力学实验工作(何斌等,2020;雷生学等,2021)。最后,还需要特别指出的是,我国钻孔体应变仪和气压计的钟差问题也是一项值得全面普查的工作。
致谢: 审稿专家提出了诸多富有洞见的建议,对稿件质量的提升帮助很大;陕西省地震局张国强博士提供了江苏省钻孔体应变和气象观测数据,在此一并表示诚挚感谢。
顾荣直、田心如、禹梁玉等, 2024, 江苏寒潮天气过程风险预评估方法研究, 气象学报, 82(2): 247-256. |
何斌、江昊琳、章东等, 2020, 基于单轴压缩实验的钻孔应变仪岩芯力学性质的研究, 地震学报, 42(6): 697-706. |
雷生学、刘建波、闫伟等, 2021, 岩体完整性对载荷干扰定量分析的影响——以天津小辛庄应变为例, 地震地质, 43(6): 1600-1613. DOI:10.3969/j.issn.0253-4967.2021.06.014 |
吕品姬、李正媛、孙伶俐等, 2022, 2022年汤加火山喷发对中国大陆地应变观测的影响分析, 武汉大学学报·信息科学版, 47(6): 927-933. |
苏恺之、刘瑞民、裴玉珍, 1993, 中国的三种体积式应变仪, 内陆地震, 7(2): 151-157. |
佟国刚、刘继庆、甄宇同等, 2005, 地震前兆数字化观测系统常见故障的分析与处理, 东北地震研究, 21(1): 31-36. |
杨小林、储日升、危自根等, 2021a, 钻孔体应变对气压和固体潮响应的传递函数——以陕西地区为例, 地球物理学报, 64(8): 2749-2765. |
杨小林、杨锦玲, 2021b, 华东地区钻孔体应变对飑线天气过程响应的特征与机制, 地震, 41(4): 180-191. |
杨小林、危自根、杨锦玲, 2023, 洞体应变对高频气压波响应的传递函数——以陕西宁强台为例, 中国地震, 39(2): 377-384. |
张凌空、牛安福, 2019, 周期气压波对地壳岩石应变测量影响的理论解, 地球物理学进展, 34(4): 1366-1370. |
朱姜韬、路瑶、李艳, 2022, 1970—2019年中国大陆地区寒潮年代际变化及大气环流成因, 兰州大学学报(自然科学版), 58(3): 337-355. |
吉田明夫、二瓶信一、太田金房等, 1984, 静岡と網代における体積ひずみ観測孔内の水位変化とひずみ変化, 気象研究所研究報告, 35(4): 199-207. |
Benioff H, 1935, A linear strain seismograph, Bull Seismol Soc Am, 25(4): 283-309. |
Borcherdt R D, Johnston M J S, Glassmoyer G, 1989, On the use of volumetric strain meters to infer additional characteristics of short-period seismic radiation, Bull Seismol Soc Am, 79(4): 1006-1023. |
Canitano A, Bernard P, Linde A T, et al, 2014, Correcting high-resolution borehole strainmeter data from complex external influences and partial-solid coupling: the case of Trizonia, Rift of Corinth(Greece), Pure Appl Geophys, 171(8): 1759-1790. DOI:10.1007%2Fs00024-013-0742-2 |
Hsu Y J, Chang Y S, Liu C C, et al, 2015, Revisiting borehole strain, typhoons, and slow earthquakes using quantitative estimates of precipitation-induced strain changes, J Geophys Res: Solid Earth, 120(6): 4556-4571. |
Huang N E, Wu Z H, 2008, A review on Hilbert-Huang transform: method and its applications to geophysical studies, Rev Geophys, 46(2): RG2006. |
Kroner C, Jahr T, Kuhlmann S, et al, 2005, Pressure-induced noise on horizontal seismometer and strainmeter records evaluated by finite element modelling, Geophys J Int, 161(1): 167-178. |
Linde A T, Suyehiro K, Miura S, et al, 1988, Episodic aseismic earthquake precursors, Nature, 334(6182): 513-515. |
Liu C, Linde A T, Sacks I S, 2009, Slow earthquakes triggered by typhoons, Nature, 459(7248): 833-836. |
Nakao S, Linde A T, Miura S, et al, 1989, Nonlinear barometric response of borehole strainmeters and its interpretation, J Phys Earth, 37(6): 357-383. |
Sacks I S, Suyehiro S, Evertson D W, 1971, Sacks-Evertson strainmeter, its installation in Japan and some preliminary results concerning strain steps, Papers Meteorol Geophys, 22(3-4): 195-208. |
Sacks I S, Suyehiro S, Linde A T, et al, 1982, Stress redistribution and slow earthquakes, Tectonophysics, 81(3-4): 311-318. |
Tsai V C, Kanamori H, Artru J, 2004, The morning glory wave of southern California, J Geophys Res, 109: B02307. |
Voight B, Hidayat D, Sacks S, et al, 2010, Unique strainmeter observations of Vulcanian explosions, Soufrière Hills Volcano, Montserrat, July 2003, Geophys Res Lett, 37(19): L00E18. |
Wang W C, Ma Y X, Qin P P, et al, 2023, Assessment of mortality risks due to a strong cold spell in 2022 in China, Front Public Health, 11: 1322019. |
Yang X L, Chu R S, Yang J L, et al, 2021, Transfer functions of borehole dilatometer responses to atmospheric loading from low-to high-frequency bands: a systematic study in Mainland China, Pure Appl Geophys, 178(9): 3559-3579. DOI:10.1007/s00024-021-02831-x |
Yoshikawa S, Koizumi T, Furuya I, 1992, Stepwise variations of strain observed by two strainmeters installed in nearby boreholes in a fracture zone, Papers Meteor Geophys, 43(1): 1-16. |
Yoshikawa S, Yamamoto T, Kamigaichi O, et al, 2001, Strain measurement by double coaxial borehole strainmeters at Odawara, Japan, J Geod Soc Japan, 47(1): 128-133. |
 2024, Vol. 40
2024, Vol. 40


