2. 辽宁省近海桥隧工程重点实验室, 辽宁大连 116023
2. Liaoning Key Laboratory of Marine Environment Bridge and Tunnel Engineering, Dalian 116023, Liaoning, China
下承式钢管混凝土系杆拱桥以其良好的力学性能、优美的外形和对不同地形的适应性,在我国桥梁建设中得到了广泛的应用(陈宝春,1997)。近断层地震动具有速度脉冲、上盘效应和方向性效应等特点,其对拱式结构桥梁的安全问题(如拱肋、桥墩的破坏等)产生了严重威胁。因此,研究下承式拱桥在近断层地震作用下的抗震性能具有重要意义。
近年来,许多学者对桥梁结构在地震动作用下结构的响应进行了研究,杜骞等(2018)比较钢管混凝土拱桥拱肋的拱脚时程曲线和拱顶时程曲线,探讨了拱肋关键截面的屈服机理;李晓莉等(2018)基于汶川地震中拱式体系桥梁的震害,以钢管混凝土桥梁为背景,总结了拱式体系桥梁的抗震性能和减隔震设计;李勇等(2019)对一座钢管混凝土拱桥进行缩尺模型实验,对桥梁结构的受力性能进行评价;谢开仲等(2021)通过有限元分别计算钢管混凝土拱桥各构件的抗震能力,提出了一种评估方法量化钢管混凝土拱桥的抗震性能;毛燕等(2023)以地震模拟振动台实验为例,根据热力学观点提出一种动力稳定分析方法,对钢管混凝土拱桥进行抗震稳定分析。
王领等(2023)对比球型钢支座和摩擦摆支座的减隔震效果,揭示了不同方案下两种支座的抗震性能变化规律。彭益华等(2022)研究了在中承式钢管混凝土拱桥中黏滞阻尼器的减震设计,对比了设置黏滞阻尼器前后桥梁结构的地震响应。戴胜勇等(2023)研究了摩擦摆支座、钢阻尼器和粘滞阻尼器在不同布置形式下对高烈度地区中承式钢管混凝土拱桥地震响应的影响。
上述学者利用实验或数值模拟对桥梁的地震响应和抗震性能进行了研究,但是近断层地震动含有很多复杂特性,不同近断层地震动输入模式或采用不同类型的近断层地震动可能导致桥梁地震响应分析结果出现偏差。在桥梁抗震分析中,改变原始桥梁结构设置减震方案同样具有一定的工程意义。因此,本文基于桥梁专业有限元分析软件Midas Civil,结合下承式钢管混凝土系杆拱桥的结构特点,分析近断层地震动输入模式、脉冲特性和竖向地震动特性等对下承式钢管混凝土系杆拱桥地震响应的影响;采用摩擦摆支座和粘滞阻尼器作为减震装置,分别研究两种减震装置对近断层下承式钢管混凝土系杆拱桥的地震响应影响。
1 近断层地震动特点及地震波选择 1.1 近断层地震动特点对于近断层的定义,目前国内外学者多数认为,若地震动记录的断层距小于20km,则认为该地震动为近断层地震动(陈笑宇等,2021)。近断层地震动主要表现出上盘效应、滑移效应、脉冲效应和方向性效应。近场地震动区别远场地震动在于近场地震动可能会包含一个明显的速度脉冲,与近断层脉冲型地震动关联的工程问题也逐渐被学者们重视,很多国内外学者进行了关于识别脉冲型地震动的研究。杨福剑等(2019)基于小波包技术,建立了脉冲模型参数预测方程模拟脉冲型地震动。冯俊等(2022)通过Butterworth非因果低通滤波器和零点法给出了脉冲型地震动的识别标准。李晓莉等(2023)基于小波理论,研究了大跨度桥梁的选波方法。Baker(2007)基于小波分析方法,利用多贝西第4阶小波作为母波,通过连续小波变换对地震动速度时程进行处理,将地震动残余能量与原始能量之比作为标准,提出了识别脉冲型地震动的指标PI(Pulse Indicator),认为PI大于0.85时的地震动为脉冲型地震动,指标计算如公式如下
| PI=11+e−23.3+14.6( PGV ratio )+20.5( energy ratio ) | (1) |
式中,PGV ratio代表地震动速度时程残余峰值与原始地震动速度峰值的比值,energy ratio代表残余函数能量与原始能量的比值。除此之外,Baker(2007)还给出了另外2个指标:①脉冲能量增加到10%的时间早于原始地震动总能量增加到20%的时间;②原始PGV大于30cm/s。根据这三个标准,可以定量判断该地震动是否为脉冲型地震动。
20世纪末发生了几次强烈的地震,如美国北岭地震、日本阪神地震和中国台湾集集地震,在这些地震中获得了大量的近断层地震动数据,研究人员对数据进一步研究发现,近断层地震动中包含强烈的竖向地震动效应(孙治国等,2022)。近年来,竖向地震动特性引起的工程问题也受到关注,李宁等(2022)建立了考虑震源特性的人工合成近断层竖向地震动的方法,并且发现我国规范建议的竖向地震动加速度与水平加速度峰值比为2/3会低估竖向地震动效应(李宁等,2020)。综上所述,研究竖向地震动和脉冲效应对下承式钢管混凝土拱桥的影响具有重要意义。
1.2 近断层地震波的选择从美国太平洋地震工程研究中心地震记录数据库(PEER)中分别筛选7条脉冲型地震动和7条非脉冲型地震动,用于对比脉冲效应对下承式钢管混凝土系杆拱桥的影响。脉冲型与非脉冲型地震动具体参数,见 表 1和表 2。
| 表 1 脉冲型地震动基本参数 |
| 表 2 非脉冲型地震动基本参数 |
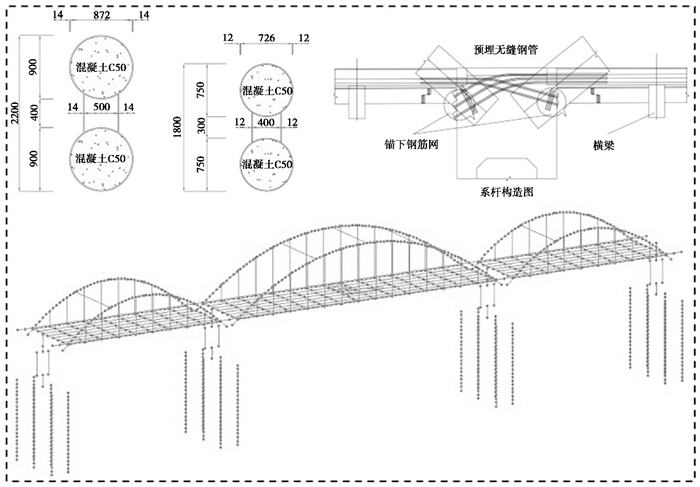
福建泉州百崎湖大桥为三跨下承式钢管混凝土哑铃型刚架系杆拱桥。主桥孔跨为51m+80m+51m,主、边跨拱轴线均为悬链线式,拱轴系数1.167,主跨矢跨比1/5,边跨矢跨比1/4.5。横桥向两幅桥独立且完全对称,单幅桥面总宽21.2m。每幅桥设有2片拱肋,拱肋间距为17.9m。
中孔和边孔拱肋均采用两根圆钢管混凝土组成的竖向哑铃型截面,管内填充C50混凝土,由钢腹板连接两根钢管成整体,腹腔内不填充混凝土。中跨两片拱肋之间设置3根“一”字型横撑,边跨两片拱肋之间设置2根“一”字型横撑,横撑均采用由圆钢管和钢腹板组成的竖向哑铃型截面。中拱与边拱的每根拱肋下设置系杆,在系杆处设两道T型纵梁将横梁彼此串联,保证桥面系的整体性。主跨、边跨均间距5m布置吊杆。桥墩采用门式框架墩结构,φ200钢筋砼钻孔灌注桩基础。
采用专业桥梁有限元分析软件Midas Civil建立百崎湖大桥模型,如 图 1所示。钢管混凝土的模拟使用软件中的截面特性计算器功能实现,吊杆采用桁架单元模拟,吊杆的初拉力利用最小弯曲能量法求得。桥面板采用板单元进行模拟,其余部分采用梁单元模拟。桩土作用利用“m法”进行计算,模型中沿桩身间距1m设置等效弹性支撑。对于钢管混凝土拱肋的本构关系,采用随动硬化本构模型;对于系杆的本构关系,采用标准两折线本构模型。
|
图 1 全桥有限元模型 |
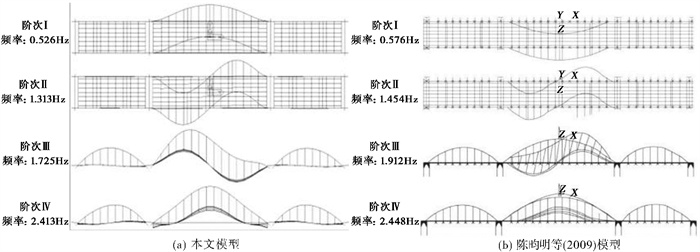
通过模态分析获得百崎湖大桥模型的振型形状与自振周期,并与陈昀明等(2009)研究中的振型与频率进行对比,对比结果如 图 2和表 3所示。可以发现,两种模型的频率误差在10%以内,振型的形状基本一致,由此初步判断本文以百崎湖大桥为背景桥建立的有限元模型是正确的。
|
图 2 振型形状对比 |
| 表 3 模型自振频率对比 |
根据百崎湖大桥地质条件和《公路桥梁抗震设计规范》(中华人民共和国交通运输部,2020)中给出的桥梁设计加速度规范谱的公式,计算E1地震作用下的标准反应谱,对有限元模型进行反应谱分析。随后对比反应谱法分析得到的结果与所筛选的近断层地震波进行线性时程分析的结果,以验证所筛选的地震波的正确性。
3.2 线性时程分析将所选取的14组地震波按照常规PGA调幅方法进行调整,水平向PGA调整至0.2g,竖向PGA调整至0.13g。将调整后的地震波按顺桥向、横桥向、竖向三向输入到模型中进行线性时程分析。
选取百崎湖大桥拱肋的18个截面,主跨和边跨各选择9个截面,截面选择从拱脚处开始,每隔L/8选择一处截面,至另一端拱脚结束。主跨截面编号Z1-1~Z9-9,边跨截面编号B1-1~B9-9,作为线性时程分析和非线性时程分析的控制截面。根据《公路桥梁抗震设计规范》规定,采用7条地震波进行线性时程分析时,结果取平均值处理,线性时程分析的结果不应小于反应谱法分析结果的80%。将线性时程分析结果与反应谱分析结果进行对比,本文所筛选的地震波的线性时程分析结果与反应谱分析结果比值满足规范要求,可以验证所筛选的地震波的正确性。
3.3 非线性时程分析非线性时程分析的截面选择与线性时程分析方法相同,在非线性时程分析中考虑三种分析工况。
第一种为对比地震动输入模式对拱桥地震响应的影响,即讨论双向输入与三向输入。根据《公路桥梁抗震设计规范》规定,应同时输入一组地震动时程的2个或3个方向分量计算地震作用效应。考虑以下两种情况:①采用所选地震动的2个分量,即纵桥向(X 向)与竖向(Z 向)输入;②用所选地震动的3个分量,沿X 向、Y 向和Z 向(竖向)输入。按照Ⅷ度区对应的基本地震动峰值加速度,将地震动峰值加速度最大的分量调整至0.4g,其余分量按照同一调幅系数进行调幅。在进行地震动输入时,横桥向(Y 方向)对应地震动时程水平分量记录中的最大PGA时程,纵桥向(X 方向)采用另一时程分量进行输入。
选取1979年英佩利尔谷地震中“El Centro Array #10”站台(断层距8.6km)记录的2个水平分量(E10050和E10320)与竖向分量(E10-UP)作为地震动输入,考虑工况如 表 4所示。
| 表 4 地震动输入方向对比工况 |
第二种为对比脉冲型地震动和非脉冲型地震动对拱桥地震响应的影响。将所筛选的7组脉冲型地震动和7组非脉冲型地震动输入到桥梁模型中,地震动输入模式均采用三向输入模式,对比分析结果。
第三种为对比竖向地震动效应对拱桥地震响应的影响。为避免脉冲效应可能会对结果产生干扰,用所筛选的7组非脉冲型地震动作为输入,按照以下两种情况输入:①采用2个水平分量,按照X+Y模式输入;②采用3个分量,按照X+Y+Z模式输入。
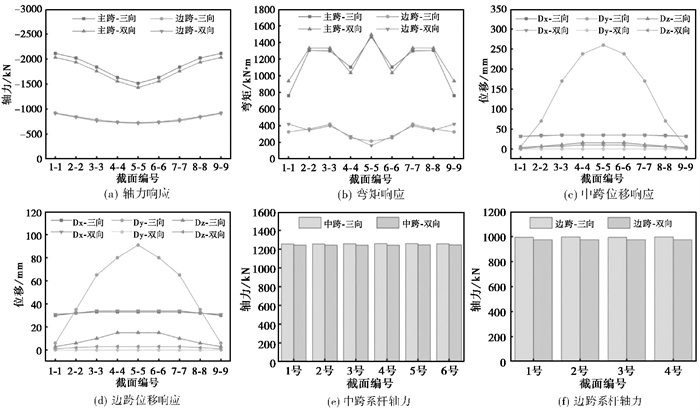
3.3.1 地震动输入模式对比图 3为拱圈在两种输入模式下的内力响应和位移响应曲线。由 图 3(a)可知,在三向输入模式下,中跨拱肋各截面轴力均大于双向输入模式,放大倍数最高为1.06。由 图 3(b)可知,三向输入模式下,拱肋各截面弯矩结果与双向输入模式相比波动幅度很小。由 图 3(c)和图 3(d)可知,在两种输入模式下,拱肋的横桥向位移结果受影响最显著;以中跨为例,工况1中拱顶截面横桥向位移为4mm,在工况2中增大到260mm。由 图 3(e)和图 3(f)可见,在不同输入模式下,系杆力的变化范围也很小,改变输入模式并未对系杆两端的相对位移产生明显影响。
|
图 3 地震动输入模式对结构地震响应的影响 |
综上所述,采用不同地震动输入模式分析获得的结果存在差异,若简单按照双向地震动输入模式分析其抗震性能,可能导致实际响应结果偏小。
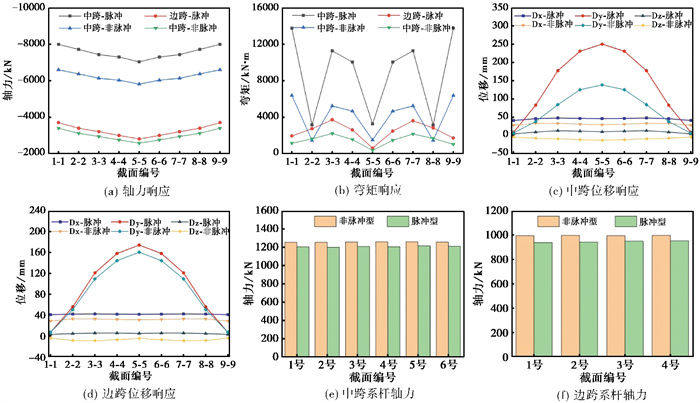
3.3.2 脉冲效应对比图 4为拱圈在脉冲型地震动和非脉冲型地震动作用下拱圈轴力、弯矩和位移响应值,定义脉冲影响系数N=Fp/Fn,其中Fp和Fn分别为脉冲型地震动和非脉冲型地震动下结构平均响应值。由 图 4(a)可知,脉冲型地震动作用下,各截面轴力整体大于非脉冲型地震动下的轴力,N值最大为1.21。由 图 4(b)可知,与轴力结果的规律相似,脉冲型地震动会放大拱圈各截面的弯矩响应,N值最大为2.15。由 图 4(c)和图 4(d)可知,脉冲效应放大了主跨、边跨拱圈的位移响应,在横桥向位移的放大效应最明显,中跨N值最大为2.17,对应位置为L/8跨处;边跨N值最大为1.11,对应位置为L/4跨处。由 图 4(e)和图 4(f)可知,在两种类型地震动作用中,系杆力的波动幅度很小。
|
图 4 脉冲效应对结构地震响应的影响 |
为讨论竖向地震动对拱桥地震响应的影响,定义竖向地震动影响系数Q,Q为竖向地震动参与后的响应值与参与前响应值的比值。
拱圈各关键截面内力与位移响应计算结果见 表 5。由表 5可知,竖向地震动对拱圈各位置的三向位移响应影响不大;竖向地震动的参与轻微降低了拱圈各位置的轴力响应而增大了弯矩响应,主跨拱顶处弯矩响应的Q值最大,为1.652,边跨弯矩响应的Q值同样在拱顶处取得最大值,为1.515。
| 表 5 拱圈地震响应竖向地震动影响系数Q |
图 5为竖向地震动参与下系杆的内力响应值,由图可知,地震作用下的系杆力对是否考虑竖向地震动的敏感性较低,考虑竖向地震动后的系杆力与不考虑竖向地震动相比波动范围很小,其原因为地震作用下系杆两端的相对位移未发生较大影响。
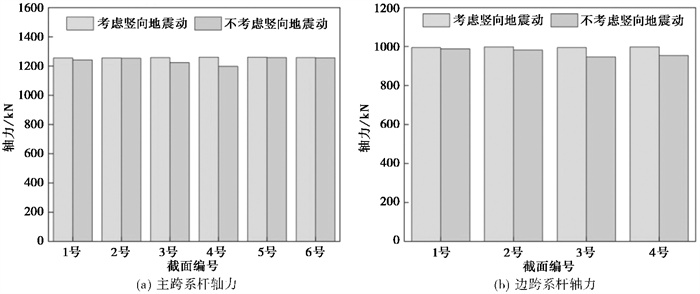
|
图 5 竖向地震动对系杆地震响应的影响 |
摩擦摆(Friction Pendulum System,FPS)减隔震装置最早由Zayas等(1990)提出,其利用单摆原理延长结构自振周期,可通过球面接触摩擦消耗能量。与传统隔震支座相比,摩擦摆支座具有更高的竖向承载力,支持更大的水平位移,且无需考虑传统隔震支座的老化、防火等问题,能够在低温环境中正常工作,可以控制摩擦摆支座的隔震周期。摩擦摆支座还具有自重轻、复位能力强等优点。随着国内外学者对其不断研究,支座构造以及材料性能不断改善,已经衍生出大量型式的摩擦摆支座,近年来得到越来越广泛的应用。
摩擦摆支座在百崎湖大桥中的布置方式如 图 6所示。
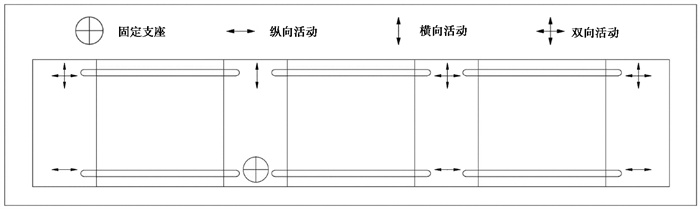
|
图 6 摩擦摆支座布置示意图 |
在Midas Civil软件中采用滞后系统模拟,通过设置弹性刚度、屈服强度、屈服指数以及滞后循环参数实现本构关系,摩擦摆支座相关参数见 表 6。
| 表 6 摩擦摆支座主要设计参数 |
截面的选取包括:①拱圈拱顶截面;②拱圈L/4截面;③系杆跨中截面;④系杆L/4截面;⑤吊杆顶部。
定义减震率为:原始结构地震响应值和减震结构地震响应值的差值除以原始结构地震响应值。图 7为主、边跨拱圈在设置摩擦摆支座前后的拱圈位移、轴力和弯矩时程曲线。由 图 7(a)和图 7(b)可知,设置摩擦摆支座能够降低拱顶位移响应,主跨原始结构位移最大值为60mm,设置摩擦摆支座后位移最大值为48mm,减震率为20%;边跨原始结构位移最大值为42mm,设置摩擦摆支座后位移最大值为36mm,减震率为14%。由 图 7(c)和图 7(d)可知,设置摩擦摆支座能够减小轴力响应,对主、边跨减震率分别为61.3%和51.1%。由 图 7(e)和图 7(f)可知,设置摩擦摆支座能够减小弯矩响应,对主、边跨减震率分别为44.5%和18.3%。
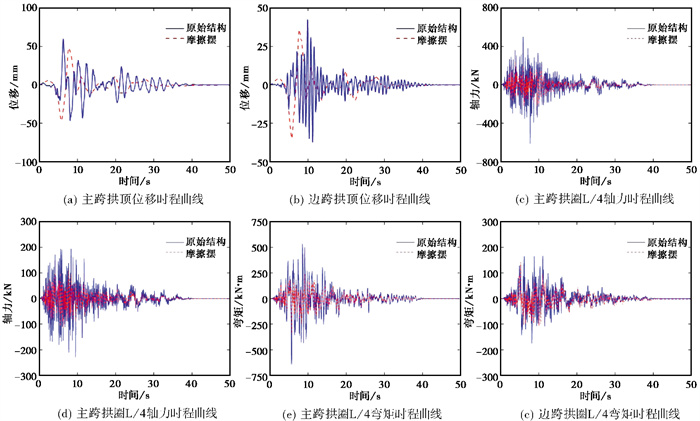
|
图 7 拱圈时程曲线对比 |
设置摩擦摆支座前后的系杆轴力结果对比如 图 8所示,西侧边跨与东侧边跨系杆在地震作用下的系杆力大致相同。西侧边跨的系杆力在997kN左右,东侧边跨的系杆力在995kN左右,说明在地震作用影响下,两边跨发生的位移变化没有很大的误差。各跨的系杆力在两种结构中没有明显的数值波动,这说明系杆构件的地震响应对于摩擦摆支座的敏感性较低。与系杆初始拉力比较,各跨系杆在地震作用下的系杆力均低于系杆初拉力,但可以看到含摩擦摆支座结构的系杆力要略大于原始结构,含摩擦摆支座结构系杆力的损失率比原始结构降低约0.7%,这说明摩擦摆支座可以轻微降低系杆初拉力的损失。

|
图 8 系杆轴力结果对比 |
设定摩擦系数分别为0.03、0.04、0.05和0.06,研究不同摩擦系数的摩擦摆支座对百崎湖大桥地震响应的影响。图 9为不同摩擦系数下拱圈的地震响应变化曲线,由图可知,主跨、边跨拱顶截面的轴力响应随摩擦系数增大而增大,弯矩响应则随摩擦系数增大而减小。摩擦系数的改变并不会对拱顶位移产生明显变化。
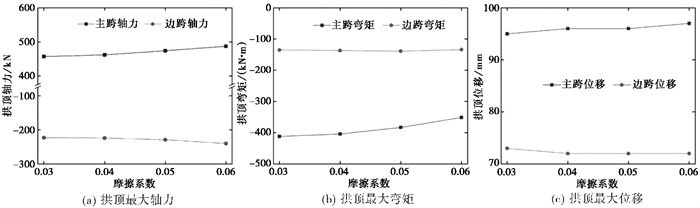
|
图 9 摩擦摆支座参数对百崎湖大桥地震响应的影响 |
粘滞阻尼器常见于斜拉桥的减隔震设计方案,其工作原理为
| F=Cvα | (2) |
其中,F为阻尼力,C为阻尼系数,v为活塞运动速度,α为阻尼指数。
在Midas Civil软件中,采用Maxwell模型模拟粘滞阻尼器,阻尼系数设置为10000kN/(m/s)α,阻尼指数设置为1.0。粘滞阻尼器布置在主跨和边跨的横撑与拱肋之间,与横撑共同构成“K”型,布置方式如 图 10所示。

|
图 10 粘滞阻尼器布置示意图 |
截面的选取包括:①拱圈拱顶截面;②拱圈L/4截面;③系杆跨中截面;④系杆L/4截面;⑤吊杆顶部。
设置粘滞阻尼器前后拱圈的内力时程曲线对比,如 图 11所示。由图可见,设置粘滞阻尼器能够降低拱圈结构的地震响应,主跨轴力减震率为61%,边跨轴力减震率为23%,主跨弯矩减震率为52%,边跨弯矩减震率为46%。
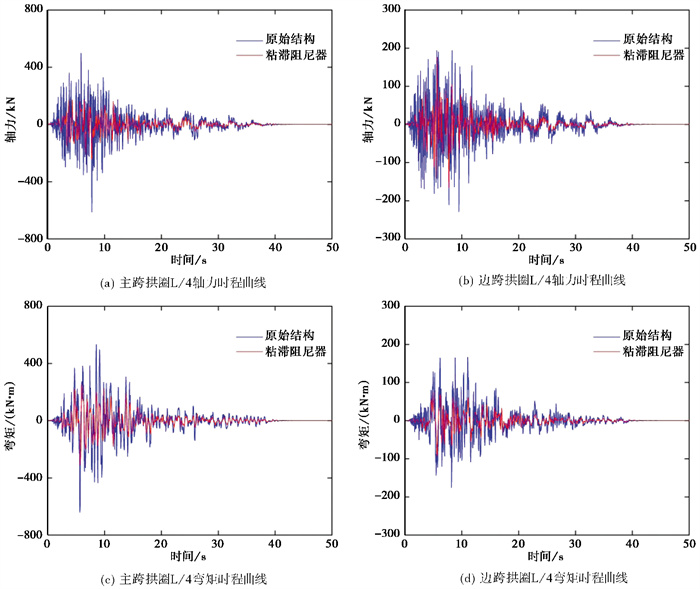
|
图 11 拱圈时程曲线对比 |
设置粘滞阻尼器前后系杆的轴力结果对比,如 图 12所示,系杆力表现出的变化规律与 图 8中的规律类似。系杆力在含粘滞阻尼器结构和在原始结构中的结果没有很大的变化,变化幅度小于1%。其原因是粘滞阻尼器布置在上部结构的拱肋与横撑之间,在地震作用中对系杆两端锚固点的相对距离的影响很弱。原始结构中系杆力的损失率在7%~10%之间,粘滞阻尼器由于能够在工作时消耗地震传递的能量,含粘滞阻尼器结构中系杆力的损失率在6%~9%之间。
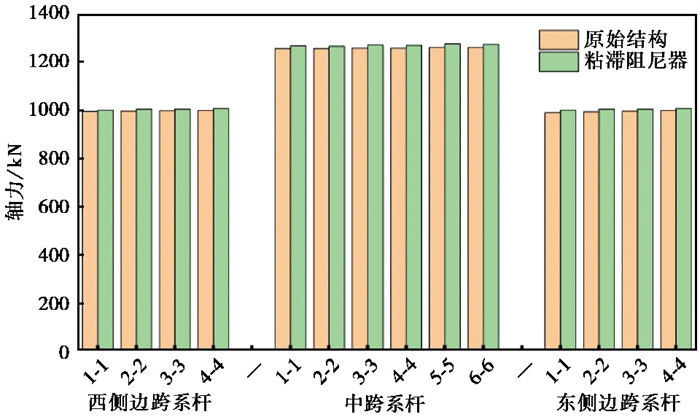
|
图 12 系杆轴力结果对比 |
(1) 双向输入模式和三向输入模式对拱肋的横桥向位移响应影响最大,三向输入模式放大了拱肋各截面的横桥向位移。总体而言,在桥梁抗震设计和计算中采用三向地震动输入模式偏于安全。
(2) 近断层地震动的脉冲效应会对下承式钢管混凝土系杆拱桥的横桥向位移产生较大影响,和非脉冲地震动相比,脉冲型地震动对拱圈横桥向位移的放大系数最大,为2.17。
(3) 近断层地震动的竖向地震动效应对拱圈位移响应的影响不大,但放大了弯矩响应结果,主跨和边跨的影响系数分别为1.652和1.515。
(4) 摩擦摆支座和粘滞阻尼器的设置均可以帮助提高桥梁的抗震性能,摩擦摆支座的设置可对拱圈的抗震性能最大提升61.3%,布置粘滞阻尼器可对拱圈的抗震性能最大提升61%。拱顶的地震位移响应对摩擦系数的敏感性偏弱,增大摩擦系数可以降低拱顶的弯矩响应结果。对于多跨下承式钢管混凝土系杆拱桥而言,采用摩擦摆支座以及粘滞阻尼器提高桥梁的抗震储备是可行的。
陈宝春, 1997, 钢管混凝土拱桥发展综述, 桥梁建设, 27(2): 8~13, 22. |
陈笑宇、王东升、付建宇等, 2021, 近断层地震动脉冲特性研究综述, 工程力学, 38(8): 1~14, 54. |
陈昀明、韦建刚、陈宝春, 2009, 泉州百崎湖大桥静动载实验分析研究, 公路工程, 34(5): 104-108. |
戴胜勇、张敏、陈克坚等, 2023, 铁路大跨度中承式钢管混凝土拱桥抗震设计, 铁道工程学报, 40(4): 50~54, 73. |
杜骞、夏修身、孙学先, 2018, 大跨度钢管混凝土拱桥非线性抗震性能研究, 地震工程学报, 40(2): 206-212. |
冯俊、赵伯明、赵天次, 2022, 基于非因果滤波和零点法的近断层脉冲型地震动识别方法, 振动与冲击, 41(19): 71-79. |
李宁、刁泽民、李忠献, 2022, 考虑震源和场地特征的近断层地区竖向地震动合成研究, 工程力学, 39(6): 181-190. |
李宁、刘洪国、刘平等, 2020, 近断层竖向地震动特征统计分析, 土木工程学报, 53(10): 120-128. |
李晓莉、赵月敏、邹积娜等, 2023, 基于小波变换的长周期桥梁选波方法研究, 中国地震, 39(4): 795-809. DOI:10.3969/j.issn.1001-4683.2023.04.008 |
李晓莉、邹雨鹤、王东升, 2018, 强震下拱式体系桥梁震害特征及抗震研究, 世界地震工程, 34(2): 33-43. |
李勇、赵晓莎、陈彦江等, 2019, 钢管混凝土拱桥缩尺模型静动力实验研究, 公路, 64(3): 99-106. |
毛燕、韩旭、李鹏飞等, 2023, 地震荷载作用下钢管混凝土拱桥的动力稳定分析方法, 公路, 68(3): 219-225. |
彭益华、毛立敏, 2022, 半漂浮式主梁钢管混凝土拱桥黏滞阻尼器减震设计, 建筑科学与工程学报, 39(2): 36-43. |
孙治国、王严信、王东升等, 2022, 近断层竖向地震动下双层桥梁排架墩抗震性能分析, 应用基础与工程科学学报, 30(6): 1494-1504. |
王领、周建庭、张瑞杰等, 2023, 大跨上承式钢管混凝土拱桥摩擦摆减隔震方案优化分析, 工程抗震与加固改造, 45(5): 112-121. |
谢开仲、王红伟、梁栋, 2021, 基于强度和延性的钢管混凝土拱桥抗震性能评估方法, 桥梁建设, 51(2): 26-33. |
杨福剑、王国新, 2019, 一种改进的近断层脉冲型地震动模拟方法, 震灾防御技术, 14(3): 489-500. |
中华人民共和国交通运输部. 2020. JTG/T 2231-01-2020公路桥梁抗震设计规范. 北京: 人民交通出版社.
|
Baker J W, 2007, Quantitative classification of near-fault ground motions using wavelet analysis, Bull Seismol Soc Am, 97(5): 1486-1501. |
Zayas V A, Low S S, Mahin S A, 1990, A simple pendulum technique for achieving seismic isolation, Earthq Spectr, 6(2): 317-333. |
 2024, Vol. 40
2024, Vol. 40


