矿产资源开采在我国经济社会发展中扮演着举足轻重的角色,而矿山炸药的使用则是不可或缺的重要环节。尽管国内工程爆破技术经历了质的飞跃,但由于对炸药爆炸能量的精确控制仍然存在挑战,部分爆炸能量仍可能以危险的形式影响周围环境。近年来,随着矿山深度的增加和开采规模的扩大,由炸药引发的爆炸事件频率和强度也呈上升趋势,给矿山安全生产带来了严峻挑战(张达等,2021)。
与天然地震传播机理类似,矿山爆炸引起的振动也是以地震波的方式向远处传播(江文彬等,2020),通过区域地震监测台网对其进行监测。通过分析台网记录到的地震波形,可以将其与天然地震事件区分,同时确定爆炸发生的时间、位置以及地震波震级,并估算爆炸当量。爆炸当量是指爆炸释放的能量,通常以等效于TNT(三硝基甲苯)爆炸所释放的能量来表示,是评估炸药或其他爆炸物品释放能量大小的重要参数。爆炸事件发生后,部分爆炸能量转化为地震波传播,对周围建筑与地层产生类似天然地震的影响(刘瑞丰等,2019)。如近几年发生的山东省龙郓煤业冲击地压事故、江苏省响水化工厂爆炸事故与河南省三门峡市河南煤气集团义马气化厂爆炸事故,均造成了重大人员伤亡与经济财产损失。因此,在爆炸事件发生后,迅速估算爆炸当量至关重要,这有助于评估其对矿山安全生产的影响,以便及时开展应急救援工作。
利用地震学方法估算爆破当量一直是地震学研究的重点(Murphy,1996;Zhang et al,2013;林鑫等,2016)。估算当量受到多种因素的影响,包括震源特征、爆炸事件埋深、传播路径、能量衰减以及地壳结构的不均匀性等(孔韩东等,2018;刘瑞丰等,2018;袁乃荣等,2018)。目前常用的估算方法主要分为两种。一种是根据经验公式,经验公式的确定一般是基于历史数据和经验规律,即利用已知炸药当量的爆炸事件找出关系式,据此估算其他待测事件的当量。由于当量是决定爆炸能量大小的直接因素,而震级通常是根据地震波在地球内部传播的振幅大小来确定的,其是对地震释放总能量的一种量化表示。因此,通常通过建立当量-震级间的经验关系式来估算爆炸当量。另一种方法是利用爆炸的地震效率进行估算,该方法是通过震级计算出地震波能量,然后利用爆炸地震效率估算出爆炸当量。其中,爆炸地震效率是指地震波能量占爆炸总能量的比例,该值的确定是本方法估算当量的关键。不同埋藏方式与不同岩性环境下的爆炸,其地震效率是不同的,例如,地下爆炸大于地上爆炸,花岗岩大于沉积岩。要精确估算当量,需要确定不同震源物理环境下的爆炸地震效率。由于当前尚未根据不同爆破作业方式与不同埋藏深度建立对应的当量估算方法,因此,为精确估算矿山爆炸当量,本文将内蒙古黑岱沟露天煤矿作为研究对象,基于内蒙古地震监测台网记录到的该煤矿爆炸事件,采用震级-当量经验公式法与爆炸地震效率两种手段研究矿山爆炸当量的估算方法。
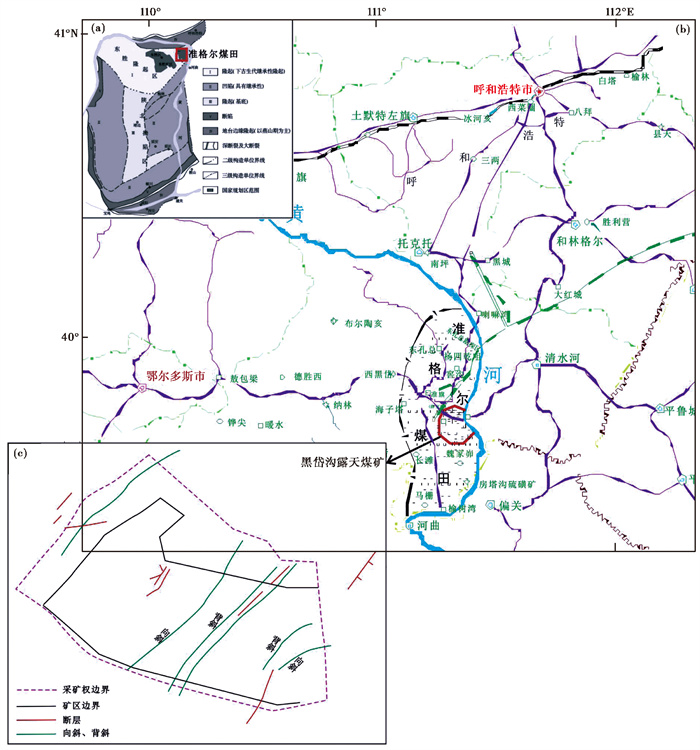
1 矿区概况与监测背景准格尔煤田地处鄂尔多斯黄土高原东部,地形复杂,总体构造轮廓呈现西北高东南低的特点,地质构造上位于华北地台鄂尔多斯盆地东北部。该地区地质构造形态复杂,主要呈现出东部隆起、西部拗陷的单斜构造,走向大致近SN,向西倾斜。地层以陆相、河湖相的二叠系—石炭系地层为主,岩性主要包括砂岩、砂砾岩和泥岩等。黑岱沟露天煤矿位于准格尔煤田中东部(图 1),隶属于中国神华集团准格尔能源有限责任公司。作为国家“八五”计划期间的重点项目之一,黑岱沟煤矿是我国自行设计、自行施工的特大型露天煤矿①。矿区地处准格尔旗东部,属于温带大陆性气候,地表特征主要是黄河为主的树枝状冲沟和河谷。整体构造线走向为NE方向,构造形态具有东北高、西南低的特点(图 1)。主要岩性包括细(粉)砂岩、中砂岩、粗砂岩、砂页岩和泥(页)岩等。矿区总面积约50km2,可采原煤储量约14.98×108t,煤层平均厚度约28m,年产煤量可达3000万吨。黑岱沟煤矿爆破作业主要采用抛掷爆破方式,爆破埋藏深度约60m。
① https://baike.baidu.com/item/黑岱沟露天煤矿/2308101?fr=ge_ala
|
图 1 黑岱沟露天煤矿区域构造背景(a)、地理位置(b)与矿区构造分布(c) |
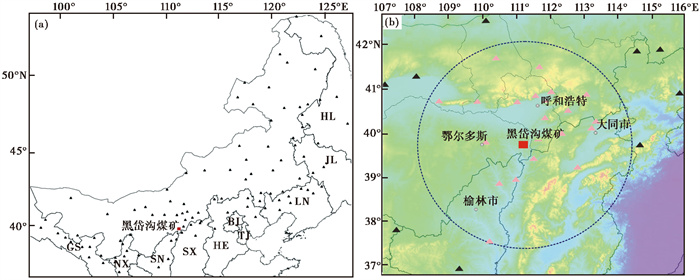
随着我国地震监测台站数量和规模的不断扩大,区域台网的监测能力得到显著提升,记录到的地震数量与种类越来越多(赵永等,1995)。内蒙古地震监测台网基于108个省内外测震台站数据(图 2),不仅可以实时监测区内及周边地区的天然地震事件,同时也可以监测到爆破、塌陷与滑坡等非天然地震事件,这意味着矿山在开采过程中实施的爆破活动也能够被台网及时监测到。根据 图 2,距黑岱沟煤矿250km内的测震台站共20个,包括宽频带、甚宽带及超宽带地震计,具有高灵敏度、大动态范围、传递函数稳定的特点,覆盖范围较好。这些台站的数据能够有效记录矿区内的爆炸事件,并准确计算爆炸事件的发生时刻、位置与震级等。目前,内蒙古地震监测台网主要通过测算地方性震级ML来描述爆炸产生的地震波能量大小,而黑岱沟煤矿则是以炸药当量来形容爆炸能量大小,由于震级与炸药当量间的相关关系尚不明确,导致一些由爆炸引起的矿山重大安全事故发生后,不能立即估算出爆炸当量,这对后期的应急救援工作造成了一定困难。
|
图 2 内蒙古地震监测台网台站分布(a)与黑岱沟煤矿250km范围内台站分布情况(b) 注:图中黑色三角形为内蒙古地震监测台网所用到的台站,蓝色虚线圆代表距黑岱沟煤矿250km的范围,粉色三角形为本文所选用的记录到黑岱沟煤矿爆炸事件的台站,红色矩形代表黑岱沟露天煤矿。 |
本文基于2020—2023年内蒙古地震监测台网记录到的且已知爆炸当量的黑岱沟露天煤矿爆破事件波形数据(共55个),选择震中距250km内的台站记录,分别采用震级-当量经验公式法与爆炸地震效应方法,开展矿山爆炸当量估算工作,以建立更加有效的矿山爆炸当量的分析方法,这一工作对于矿山安全生产的有效监管以及应急救援工作的开展具有重要意义。
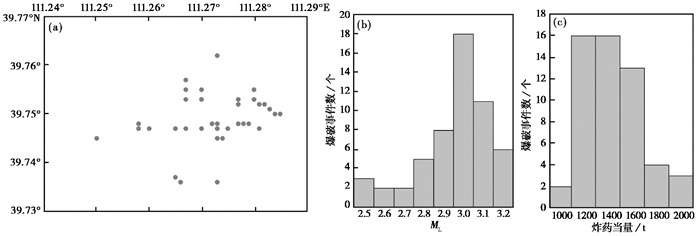
2 数据与典型震例本文选用的数据为内蒙古地震监测台网2020—2023年监测到的55起黑岱沟露天煤矿爆破作业事件,这些事件均已知实际爆炸位置与炸药当量,爆破作业方式为抛掷爆破,爆炸埋藏深度为60m。通过对所有事件波形记录的分析与测算,内蒙古地震监测台网判定所有事件均为爆破事件,并给出了所有事件的震中位置与震级值(图 3(a)、3(b))。从爆破事件的震中位置分布来看,可以观察到这些事件的位置分布较为集中,震级分布范围在ML2.5~3.2,实际炸药当量范围为774~1855t(图 3(b)、3(c))。
|
图 3 爆破事件的震中分布(a)、震级分布(b)与实际炸药当量分布情况(c) |
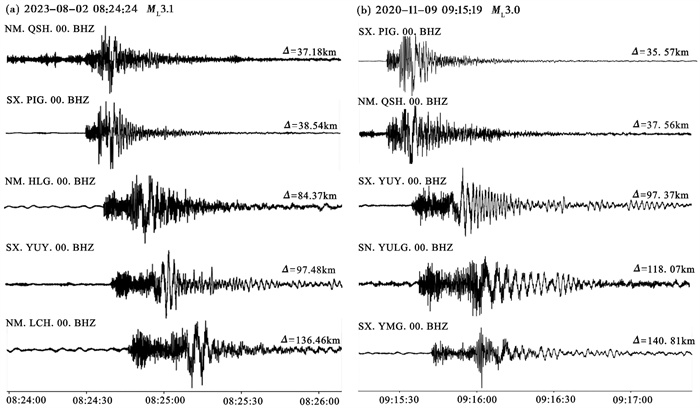
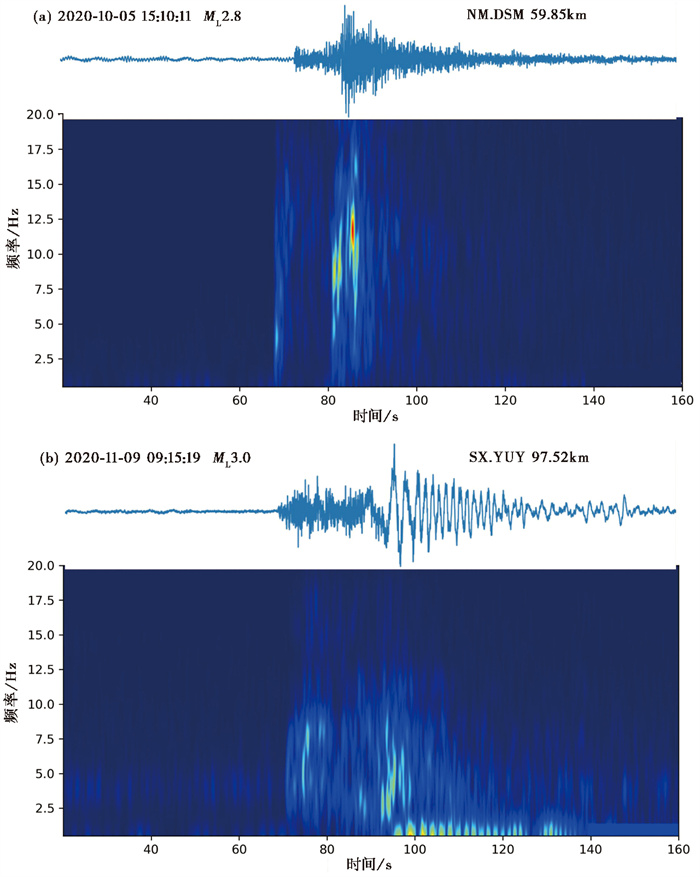
图 4给出了内蒙古地震监测台网记录到的本文55个爆破事件中典型事件的垂直向波形记录,可以观察到,黑岱沟煤矿的人工爆破事件其波形发育较清楚的P波震相,初动尖锐,P波初动方向均向上,S波欠发育,面波较发育。此外,通过分析爆破事件的时间-能量谱特征(图 5),也可以看出人工爆破的频带较窄,高频能量主要分布在5Hz以下,其P波能量偏高于S波能量,S波频带较窄。综合波形与能量谱特征的分析,可以很明显地看出黑岱沟露天煤矿爆破事件的地震记录具有典型的浅源爆炸特征。
|
图 4 内蒙古地震监测台网监测到的黑岱沟煤矿爆破事件的波形记录 注:(a)发震时刻为2023年8月2日8时24分11秒;(b)发震时刻为2020年11月9日9时15分19秒);图中波形开始与末尾为相应的地震台站与震中距(时间UTC)。 |
|
图 5 内蒙古地震监测台网监测到的黑岱沟煤矿爆破事件的时间-能量谱特征 注:(a)发震时刻为2023年8月2日8时24分11秒;(b)发震时刻为2020年11月9日9时15分19秒。 |
当量是评估爆炸释放的能量大小的重要参数。然而,当无法获取爆炸现场冲击波数据时,直接计算准确的爆炸当量变得十分困难(王志宇等,2023)。为解决这一问题,本文利用已知炸药当量的爆炸事件的地震波数据,尝试通过震级与当量经验公式以及爆炸地震效率两种手段,寻找适用于矿山爆炸当量估算的方法。
3.1 根据爆炸地震效率估算爆炸当量经研究,人们发现通过测量地震波形记录的振幅信息,可以计算出地震波的能量(Gutenberg et al,1954),如,Gutenberg等(1942)提出的震级-能量关系式,即
| lgEe=11.3+1.8ML | (1) |
式中,ML为地震波地方性震级,Ee为地震波辐射能量,单位为尔格(ergs)。通过式(1),可以根据区域台网测量的地方性震级ML计算地震波能量。若Ee单位为焦耳(J),则式(1)应改为
| lgEe=4.3+1.8ML | (2) |
爆炸事件发生后,其化学能会有一部分转化为地震波能量,因此,利用爆炸产出的地震波能量可以计算出爆炸总化学能(Haskell,1967;Stroujkova et al,2015)。该方法的关键在于获取爆炸地震效率,爆炸地震效率是指爆炸释放的总能量与产生的地震能量之间的比例,其可以用来描述爆炸产生地震波的效率,通常用百分比表示,即
| k=EeEt=EeE0×Q | (3) |
式中,Et、Ee分别为爆炸总化学能与其产生的地震波能量,单位均为J;k为爆炸地震效率;Q为炸药当量,单位为kg;E0为单位千克TNT所产出的化学能,数值为4.2×106J。
可以看出,当爆炸事件发生后,根据区域地震监测台网测定的地震波地方性震级ML,利用式(2)可计算出地震波能量。在此情况下,如果已知爆炸地震效率,便可以利用式(3)估算出炸药当量。具体流程如 图 6所示。然而,爆炸地震效率与震源区的岩性、埋藏深度以及爆炸持续时间等因素密切相关(江文彬等,2020),因此,在不同的环境下发生的爆炸,其爆炸地震效率也会有所不同。

|
图 6 利用爆炸地震效率估算爆炸当量流程 |
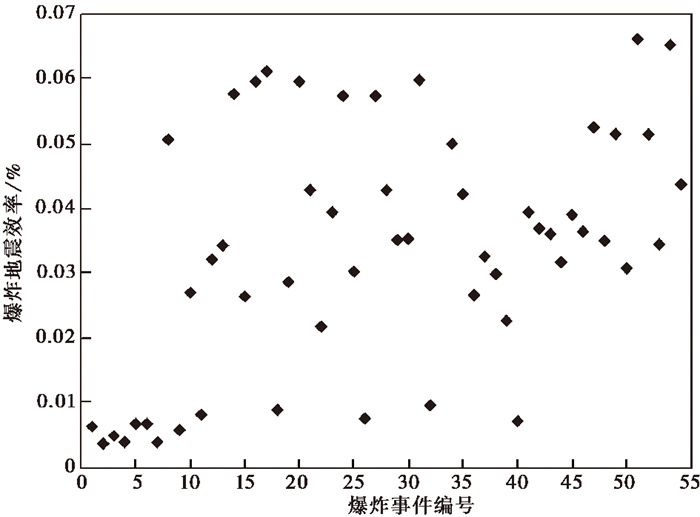
本文收集了黑岱沟露天煤矿55个已知炸药当量的ML≥2.5爆破作业事件的数据,利用内蒙古地震监测台网测定的每个爆破事件的地方性震级ML,从而得出地震波的辐射能量。基于已知的炸药当量得到了爆炸地震效率(图 7)。由 图 7可以看出本文得到的爆炸地震效率数值分布相对集中,主要分布在0.02%~0.07%之间,平均值约为0.034%。这说明在黑岱沟露天煤矿采用抛掷爆破方式(埋深60m)时,其爆炸地震效率应在0.02%~0.07%范围内。考虑到黑岱沟露天煤矿爆破作业区主要发育以煤层为主的沉积岩,本文的结果在一定程度上也反映了发生于类似沉积岩环境下、埋深约60m的爆炸事件的爆炸地震效率应该约为0.02%~0.07%。对于发生在类似环境下但当量未知的爆炸事件,可以根据本文得到的爆炸地震效率数值进行爆炸当量的估算。
|
图 7 黑岱沟露天煤矿55起爆破事件的爆炸地震效率分布 |
震级可以反映地震波辐射能量的大小,而炸药当量则直接反映了爆炸能量的大小。因此,震级-当量经验关系方法是最常用的一种估算爆炸当量的方法。许多学者通过收集核爆数据建立了震级与当量之间的经验关系式。例如,Nuttli(1986)、Patton(1988)、Ringdal等(1992)与Murphy(1996)分别建立了较大震级爆炸事件的体波震级与炸药当量之间的关系(表 1)。基于这些成果,Bowers等(2001)提出了适用于较小震级爆炸事件的体波震级与炸药当量之间的关系(表 1)。此外,刘瑞丰等(2019)基于一些已知当量的矿山爆破事件,提出了地方性震级ML与当量之间的经验关系(表 1)。通过分析已经建立的震级-当量经验关系式(表 1),可以发现,震级与炸药当量之间的关系可以表示为
| M=a×lgQ+b | (4) |
| 表 1 国内外学者建立的震级-当量经验关系 |
② 体波震级, 即采用体波(P, PP, S)测定震级, 适用于远震与深源地震.
③ 地方性震级, 也称为近震震级, 在我国适用于震中距1000km范围内的地震震级测定.
其中,M为震级,Q为炸药当量,a、b为常数。
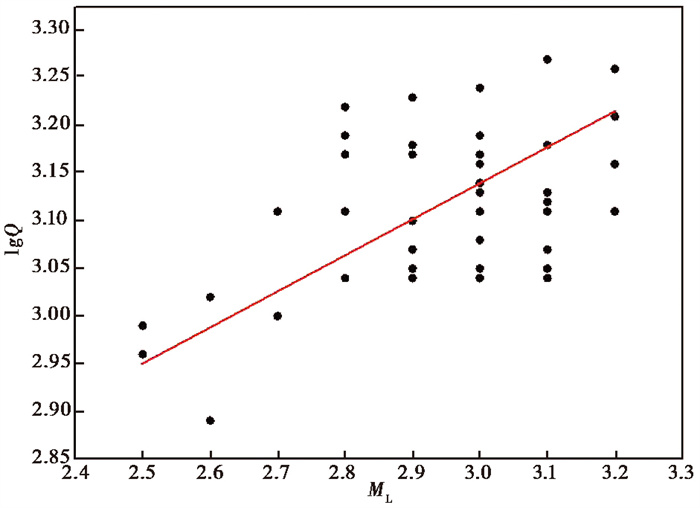
由于浅源爆炸产生的能量相对较小,导致地震波能量也相对较小,仅在近场记录中可以观测到较清晰的P波与S波震相,所以地方性震级ML对于估算矿山爆破的炸药当量较为适用。本文针对黑岱沟露天煤矿已知炸药当量的爆炸事件,根据内蒙古地震监测台网测定的地方性震级ML,使用正交回归方法得到地方性震级ML与炸药当量间的关系(图 8),并给出了二者间的经验关系式
| lgQ=0.4ML+1.94 | (5) |
|
图 8 地方性震级ML与爆破炸药当量Q之间的正交关系 |
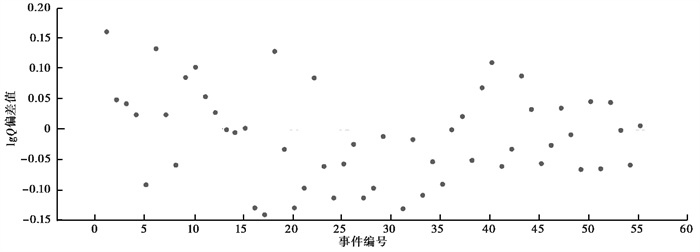
其中,Q为炸药当量,单位为吨(t)。根据图 9可以看出,式(5)针对本文所采用的55个爆炸事件的lgQ误差值在±0.15范围内,平均值为0.01,即,炸药当量Q的误差值在±250t间,平均误差值为46t。此外,基于区域台网测定的地方性震级ML(支明等,2023),利用式(5)估算了黑岱沟煤矿2条新爆炸事件的当量值(表 2),可以看出,由式(5)估算的炸药当量与实际当量值较为接近,一定程度上反映本文得到的经验公式对估算黑岱沟露天煤矿爆破事件的当量值是较为合适的。
|
图 9 55个爆炸事件基于震级-当量拟合公式(lgQ=0.4ML+1.94)的误差分析结果 |
| 表 2 由经验公式估算新爆破事件的当量值及其与实际当量的偏差 |
本文利用黑岱沟露天煤矿的爆破数据,通过爆炸能量与地震波能量的关系,得到矿山爆破的爆炸地震效率分布范围在0.02%~0.07%,这一数值可用于估算爆炸事件的炸药当量。不少学者通过实验也给出了爆炸地震效率,如Haskell(1967)提出花岗岩环境中的爆炸地震效率约为3.7%,张少泉等(1984)根据煤矿爆炸实验数据,得出硐室爆破、矿山爆破与开放性爆破的爆炸地震效率分别约为0.018%、0.06%与0.01%~0.1%,Flynn等(1988)认为化学爆炸在干燥沉积岩中的爆炸地震效率约为0.7%~1%,Ford等(2014)与Stroujkova等(2015)分别提出浅地表或地面上的化学爆炸其地震效率约为0.5%~2%、0.2%~1.9%。可以看出,不同埋深、不同岩性环境下的爆炸地震效率存在显著差异。因此在使用爆炸地震效率估算当量时,应根据埋深、发育岩性等选择合适的爆炸地震效率数值。此外,本文得到的结果与张少泉等(1984)的结果较为一致,说明本文给出的爆炸地震效率对于矿山爆破是合理的。
基于已知当量的爆炸数据,得到了矿山爆破的震级-当量经验关系,将该关系式与刘瑞丰等(2019)提出的经验关系进行对比(图 10),发现二者之间存在一定差异。造成这种差异的原因可能来自两方面,一方面可能是由于本文的爆破样本其炸药当量分布范围较小,对应测定的震级范围也较小,未能充分反映更大当量范围内的震级-当量经验关系;另一方面可能是由于本文采用的爆破数据其爆破埋深条件(埋深60m)及爆破作业方式(抛掷爆破)与刘瑞丰等(2019)收集的爆破数据(多为硐室爆破、分层秒差起爆方式)不同,导致得出的震级-当量经验关系存在一定差异。

|
图 10 本文得到的地方性震级ML与炸药当量Q之间的正交关系与前人结果对比 |
本文基于内蒙古地震监测台网记录到的黑岱沟露天煤矿已知炸药当量的爆破数据,利用地震能量与爆炸总能量间的关系以及炸药当量经验关系方法,分别从爆炸地震效率、震级-当量经验关系两个方面分析炸药当量的估算方法,得到以下认识与结果:
(1) 煤矿等矿山发生的爆破事件其爆炸地震效率约为0.02%~0.07%。在矿山爆炸发生后,根据地震监测台网测定的震级与本文得到的爆炸地震效率,可快速估算爆炸当量。需要注意的是,不同埋深、不同岩性环境下的爆炸地震效率是非常不同的,差距可达两个以上数量级,因此,在使用爆炸地震效率准确估算炸药当量时,应根据爆炸的埋深与周围发育岩性等选择适合的爆炸地震效率。
(2) 关于震级-当量关系的经验公式有很多,但多数都基于核爆实验数据,且使用的震级也多为体波震级,对于小当量爆炸事件可能不太适用。本文以黑岱沟露天煤矿为例,利用区域地震监测台网测定的地方性震级ML,建立了适用于矿山爆炸事件的震级与当量的经验关系(式5)。考虑到本文使用的爆炸数据相对局限,可能未能全面地反映更大当量范围内的震级-当量关系,此外,目前已提出的震级-当量经验公式多数都是针对特定地质环境与爆破作业方式。因此,后续将通过收集不同地质环境下、不同埋深条件的已知当量的爆炸数据,有针对性地建立更为精确的震级-当量间的经验关系。
江文彬、陈颙、彭菲, 2020, 2019年3月江苏响水化工厂爆炸当量的估计, 地球物理学报, 63(2): 541-550. |
孔韩东、王婷婷, 2018, 爆破当量研究综述, 国际地震动态, (2): 9-25. |
林鑫、姚振兴, 2016, 利用区域地震波形振幅包络约束朝鲜地下核实验的埋深和当量, 地球物理学报, 59(6): 2066-2079. |
刘瑞丰、孔韩东、李赞, 2018, 能量震级测定方法研究, 国际地震动态, (8): 56. |
刘瑞丰、李赞、张玲等, 2019, 爆炸当量估算的初步研究, 地震地磁观测与研究, 40(4): 1-7. DOI:10.3969/j.issn.1003-3246.2019.04.001 |
王志宇、郝春月, 2023, 基于海拉尔台阵资料的爆炸事件震级测定和当量估计, 地震学报, 45(6): 1079-1090. |
袁乃荣、刘瑞丰、李赞等, 2018, 能量震级及其测定, 地震地磁观测与研究, 39(5): 1-7. |
张达、戴锐、曾志毅等, 2021, BSN矿山微震监测技术及其应用, 中国地震, 37(2): 332-348. DOI:10.3969/j.issn.1001-4683.2021.02.008 |
张少泉、郭建明, 1984, 爆炸地震的能量转换系数计算及其应用, 地球物理学报, 27(6): 537-547. |
赵永、刘卫红、高艳玲, 1995, 北京地区地震、爆破和矿震的记录图识别, 地震地磁观测与研究, 16(4): 48-54. |
支明、梁建宏、孙丽等, 2023, 地震自动速报中常用震级测定方法的适用性研究, 中国地震, 39(4): 868-882. |
Bowers D, Marshall P D, Douglas A, 2001, The level of deterrence provided by data from the SPITS seismometer array to possible violations of the Comprehensive Test Ban in the Novaya Zemlya region, Geophys J Int, 146(2): 425-438. |
Flynn E C, Stump B W, 1988, Effects of source depth on near-source seismograms, J Geophys Res: Solid Earth, 93(B5): 4820-4834. |
Ford S R, Rodgers A J, Xu H M, et al, 2014, Partitioning of seismoacoustic energy and estimation of yield and height-of-burst/depth-of-burial for near-surface explosions, Bull Seismol Soc Am, 104(2): 608-623. |
Gutenberg B, Richter C F, 1942, Earthquake magnitude, intensity, energy, and acceleration(Second paper), Bull.seism.soc.am, 32(2): 105-145. |
Gutenberg B, Richter C F, 1954, Seismicity of the Earth and Associated Phenomena, 2nd ed, Princeton: Princeton University Press.
|
Haskell N A, 1967, Analytic approximation for the elastic radiation from a contained underground explosion, J Geophys Res, 72(10): 2583-2587. |
Murphy J R. 1996. Types of seismic events and their source descriptions. In: Husebye E S, Dainty A M. Monitoring a Comprehensive Test Ban Treaty. Dordrecht: Springer.
|
Nuttli O W, 1986, Yield estimates of Nevada test site explosions obtained from seismic Lg waves, J Geophys Res: Solid Earth, 91(B2): 2137-2151. |
Patton H J, 1988, Application of Nuttli's method to estimate yield of Nevada Test Site explosions recorded on Lawrence Livermore National Laboratory's digital seismic system, Bull Seismol Soc Am, 78(5): 1759-1772. |
Ringdal F, Marshall P D, Alewine R W, 1992, Seismic yield determination of Soviet underground nuclear explosions at the Shagan River test site, Geophys J Int, 109(1): 65-77. |
Stroujkova A, Leidig M, Bonner J L, 2015, Effect of the detonation velocity of explosives on seismic radiation, Bull Seismol Soc Am, 105(2A): 599-611. |
Zhang M, Wen L X, 2013, High-precision location and yield of North Korea's 2013 nuclear test, Geophys Res Lett, 40(12): 2941-2946. |
 2024, Vol. 40
2024, Vol. 40


