2. 中国地震局地震预测研究所, 北京 100036
2. Institute of Earthquake Forecasting, China Earthquake Administration, Beijing 100036, China
2020年7月,由我国自主建设运行的北斗卫星导航系统(Beidou Navigation Satellite System,BDS)正式宣布组网完成,并向全球用户提供全天候、全天时和高精度的定位、导航以及授时服务(杨子辉等,2022)。BDS-3由3颗地球静止轨道(Geostationary Orbit,GEO)卫星、3颗倾斜地球同步轨道(Inclined Geosynchronous Orbit,IGSO)卫星和24颗中圆地球轨道(Medium Earth Orbit,MEO)卫星组成,其中IGSO和GEO卫星由中国空间技术研究院(China Academy of Space Technology,CAST)研发,MEO卫星由CAST和上海微小卫星工程中心(Shanghai Engineering Center for Microsatellites,SECM)研发,BDS-3的公开服务信号除了继承BDS-2的B1I和B3I频点外,新增了B1C、B2a、B2b三个新频点(Yang et al,2019)。
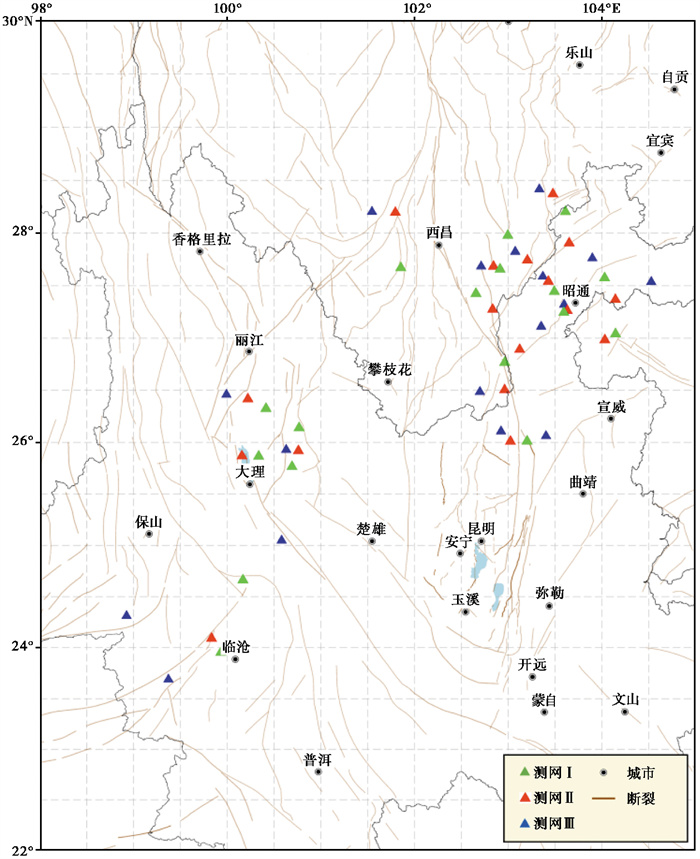
中国地震科学实验场(以下简称“实验场”)是以深化地震孕育发生规律和成灾机理的科学认识、提升地震风险的抗御能力为目的建设的地震野外实验场①。实验场范围从川甘交界到云南南部,包括青藏高原东构造结附近的川滇菱形块体及其周边,该地区受到欧亚板块与印度板块互相碰撞挤压的影响,呈现出压缩、剪切、拉张等各类复杂的地壳形变特征,地震活动异常强烈(王敏等,2020;Wang et al,2015)(图 1)。区域内曾发生2008年汶川8.0级、2013年四川芦山7.0级、2017年九寨沟7.0级等地震,均造成了严重的人员伤亡和财产损失;该区域有龙门山、鲜水河、安宁河、则木河、小江、嘉黎、怒江、红河、丽江—小金河等重要断裂带,是我国地壳变形监测与地震研究的重点地区(张致伟等,2022)。对实验场加密观测网络的GNSS数据进行精细化解算,是提取该地区同震、震间、震后、非构造变形等信息的关键,其对于区域形变特征、断层孕育物理模型的研究具有重要意义。目前,在实验场新增的200个测站中,有51个测站能够接收BDS-3观测数据,为BDS-3高精度定位领域的研究和应用提供了数据支撑。
① http://www.cses.ac.cn/sycgk/lsyg/sycjj/index.shtml.
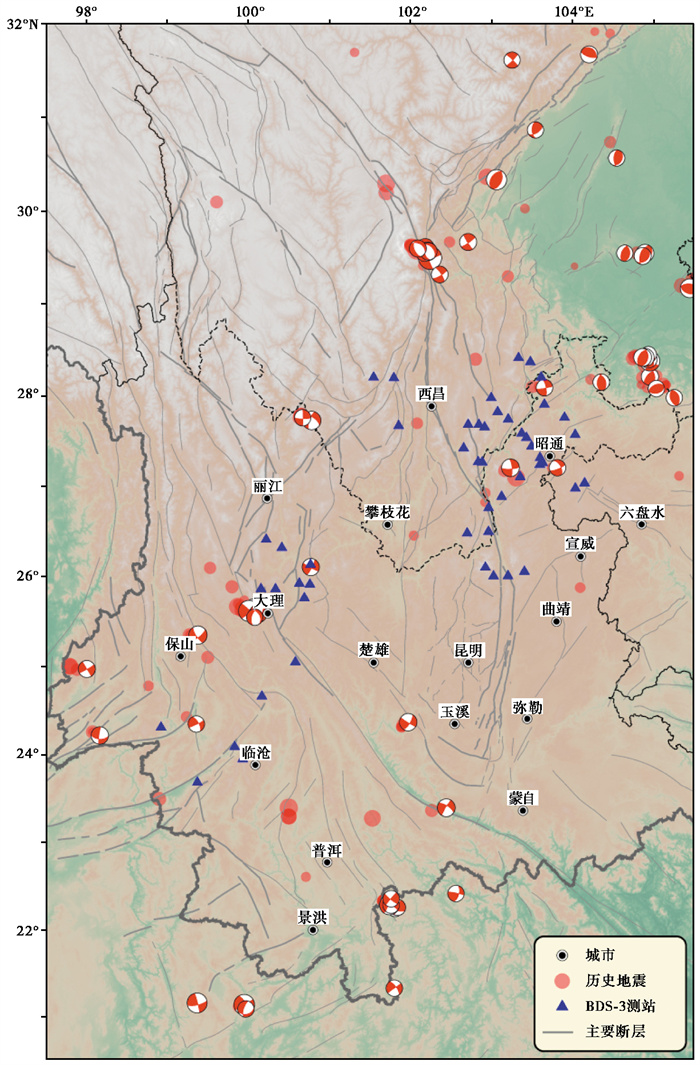
|
图 1 研究区BDS-3台站分布 |
北斗数据解算精度很大程度上依赖于数据质量与轨道精度。Shi等(2021)、王西龙等(2023)对BDS-3观测数据质量进行评估,结果表明不同类型的接收机表现出不同的抗多路径性,B1C频点受多路径及噪声的影响更为显著;李星星等(2022)综述了GNSS精密定轨的关键技术,对不同精密轨道产品中BDS-3及其他卫星系统的轨道精度进行了分析。随着北斗卫星系统的完善与发展,其在高精度数据解算与应用方面备受关注。Su等(2018)和王阅兵等(2018)对BDS-2在高精度数据解算及地壳监测进行了初步探索,结果表明精密单点定位和双差定位精度略低于GPS,但其具备在地壳变形监测领域应用的能力;Li等(2019)对BDS-2与BDS-3之间的系统间偏差进行分析,结果表明二者的公共信号B1I和B3I之间不存在明显的系统间偏差,精密定轨中可视为一个系统。与BDS-2相比,BDS-3在卫星数量、星座性能及观测频点等方面得到进一步完善,使其在高精度数据解算中更具优势。目前,大量研究主要针对BDS-2数据以及MGEX参考站BDS-3数据,对于大规模区域网BDS-3观测数据的高精度数据解算有待进一步研究。
本文基于GNSS观测数据高精度解算时常用的GAMIT/GLOBK10.71科学计算软件,从北斗卫星星座的定位性能、观测数据质量、精密星历精度以及解算参数设置4个方面对实验场北斗观测数据高精度解算影响因素进行系统性分析,为北斗大规模区域网观测数据高精度解算提供参考。
1 数据来源依托中国地震科学实验场大地测量数据中心,本文共收集51个能够接收BDS-3观测数据的测站(图 1),这些测站自2020年以来陆续安装了TRIMBLE ALLOY型接收机,并配备TRM159900.00型天线,目前可以接收GPS信号以及BDS-3包括B1I、B1C、B2a和B3I四个公开服务信号。以2022年积日(Day of Year,DOY)001的观测数据为例,进行星座定位性能和观测数据质量分析,并选取2022年DOY 001~030的观测数据进行解算方案研究,数据采样间隔为30s。通过对原始数据的进一步调查,定轨分析中心暂时不能提供GEO卫星的高精度精密轨道信息,因此,在数据分析及解算过程中剔除了GEO卫星。此外,鉴于BDS-2和BDS-3卫星均能够播发B1I和B3I信号,本文在对BDS-3数据解算前初步引入了BDS-2卫星并分析其可行性。
2 北斗定位性能及观测数据质量分析初步确定参与解算的BDS卫星星座后,通过可见卫星数和精度因子(Dilution of Precision,DOP)进一步对其定位性能进行分析,验证定位的可靠性。其次,通过分析BDS-3不同频点及卫星的信噪比和伪距多路径误差,从而筛选出观测数据质量更优的频点和卫星,为数据解算中北斗观测数据的使用提供参考。
2.1 定位性能分析以DC01测站2022年DOY001观测数据为例,对BDS卫星星座定位性能进行评价。GPS和BDS-3卫星系统可见卫星数如 图 2所示,由图可见BDS-3有72.5%历元可见卫星数在7~8颗,与GPS相比分布更为集中。整体上,两个系统所有历元的可见卫星数均在5颗以上,且60%以上历元有7~8颗卫星,满足卫星定位的基本需求(杨元喜等,2021)。
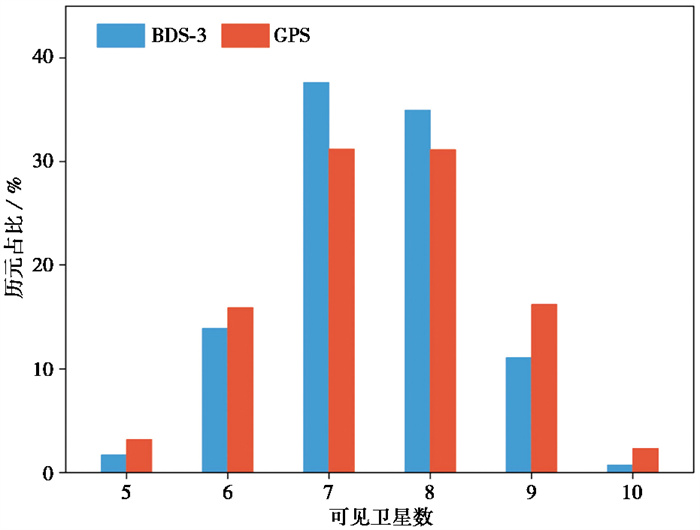
|
图 2 GPS和BDS-3可见卫星数的历元占比 |
描述卫星定位性能的一个重要指标是DOP值(吕春东等,2018),其值越小,定位精度越高。精度因子包括几何精度因子(Geometric Dilution of Precision,GDOP)、空间位置精度因子(Position Dilution of Precision,PDOP)、平面位置精度因子(Horizontal Dilution of Precision,HDOP)和高程精度因子(Vertical Dilution of Precision,VDOP)。BDS-3和GPS的四类精度因子随时间变化的曲线如 图 3所示,总体上两个系统的DOP值差异并不明显。对于大多数历元,GDOP在2~4之间,根据对应的定位精度等级(柯晔等,2021),两个系统均表现为优,PDOP保持在1.5~3.5之间,HDOP保持在0.5~1.6之间,VDOP保持在1~3之间。但在GPS个别历元中,DOP值较大,而BDS-3表现更为稳定。从平均水平来看(表 1),二者差异性很小,表明其定位性能相当。由此可见,BDS-3在完成组网后,卫星可见性和星座空间几何构型均得到进一步提升,与GPS保持在相当水平,且表现更为稳定,不会在高精度数据解算中与GPS产生系统性差异。
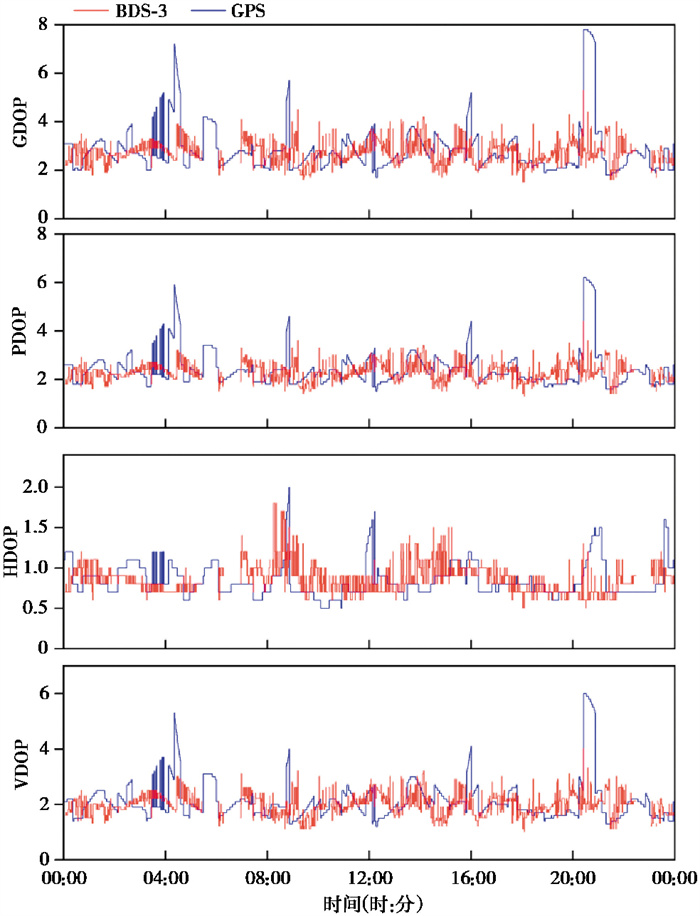
|
图 3 BDS-3和GPS的DOP值随时间的变化 |
| 表 1 BDS-3和GPS各DOP值的单天均值 |
信噪比(Signal-to-noise Ratio,SNR)是载波信号强度与噪声强度的比值,可以从观测文件中直接获取。信噪比越大,代表观测数据质量越好,其值主要受信号发射功率、接收机和天线类型等因素影响(李星星等,2022;许扬胤等,2018)。
为减弱不同测站观测环境因素对数据质量的干扰,本文统计了实验场2022年DOY 001全部有效观测测站GPS和BDS-3不同频点信噪比均值随时间的变化,结果如 图 4所示,从图中可以看出,GPS的L1和L2频点分别在41~44.6dB-Hz和35.6~42.4dB-Hz左右变化,明显低于BDS-3,且波动较大,波动幅度分别为3.6dB-Hz和6.9dB-Hz。BDS-3不同频点信噪比波动相对较平稳,且变化趋势基本相同,其中B2a的信噪比略优于B3I,分别在46.8dB-Hz和46.3dB-Hz左右变化;B1I的信噪比略优于B1C,分别在44.2dB-Hz和45dB-Hz左右变化。4个频点信噪比表现出明显的大小关系,即B2a>B3I>B1I>B1C。
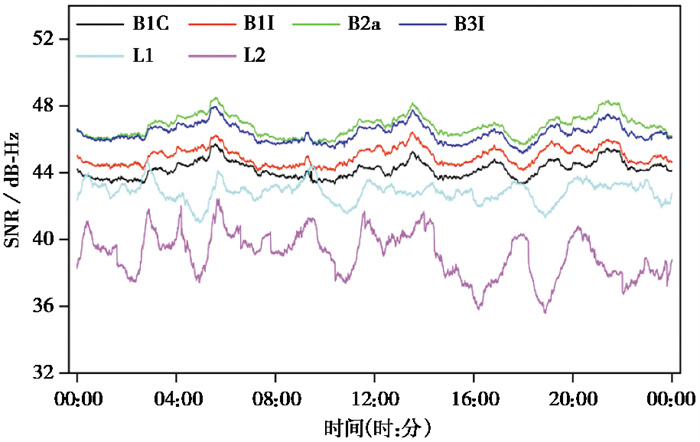
|
图 4 BDS-3和GPS各频点信噪比随时间的变化 |
此外,不同卫星的数据质量也存在一定差异。选取DC01测站2022年DOY 001观测数据,以GPS的L2和BDS的B3I频点为例,进一步对不同卫星的信噪比进行分析。图 5展示了不同卫星信噪比的天空图,与GPS相比,BDS卫星信噪比表现更稳定,受卫星高度角的影响较小。在低高度角时,GPS的信噪比低于BDS-3,在高度角较大时则相反。在数据处理中,通过设置合理的卫星截止高度角,即可剔除信噪比较差的低高度角历元。BDS-3和BDS-2(C06~C16)卫星高度角在25°以上的历元信噪比表现较优,基本均在46dB-Hz以上,不存在信噪比特别差的卫星。
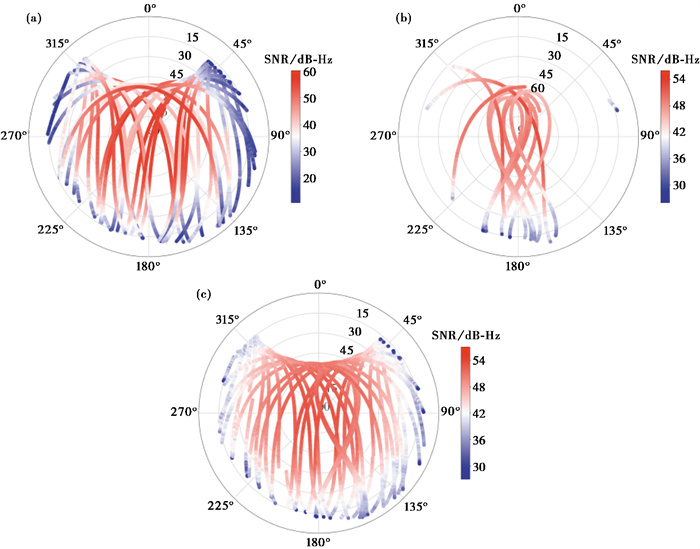
|
图 5 GPS(a)、BDS-2(b)、BDS-3(c)卫星信噪比天空图 注:GPS卫星以L2为例,BDS-2卫星以B3I为例,BDS-3卫星以B3I为例。 |
多路径效应是伪距观测的主要误差之一(杨元喜等,2021)。在高精度数据解算中,确定宽巷模糊度时需要引入伪距观测,而宽巷组合观测值必然放大伪距多路径误差,因此有必要对其进行具体分析。伪距多路径误差可以通过MP组合(赵大江等,2023)来计算。
计算实验场2022年DOY 001全部有效观测测站GPS和BDS-3不同频点伪距多路径误差均值,结果如 图 6所示。从图中可以看出,GPS与BDS-3卫星相比,GPS频点的伪距多路径误差明显小于BDS-3,L1和L2频点分别在0.23m和0.25m左右变化,说明GPS信号的抗多路径误差水平优于BDS-3,这可能是由于特定型号的接收机对不同信号接收的抑制多路径干扰能力存在差异。对于BDS-3频点,B2a伪距多路径误差明显大于其他频点,最大可达0.42m;B3I次之,在0.28~0.39m之间;B1I伪距多路径误差略大于B1C,在0.26~0.34m以内;B1C最小,与B1I差异在0.02m以内。

|
图 6 BDS-3和GPS不同频点伪距多路径误差随时间的变化 |
同样,选取DC01测站2022年DOY 001观测数据,计算GPS卫星L2和BDS卫星B3I频点的伪距多路径误差天空图,如 图 7所示。不同卫星均受到高度角的影响而出现较大的伪距多路径误差,对于小于30°的低高度角的观测历元,GPS的伪距多路径误差大于BDS,最大可达到0.8m,表明GPS卫星的伪距多路径误差受高度角的影响更为显著。与BDS-3卫星相比,BDS-2卫星的低高度角观测历元较少,大多数观测历元的伪距多路径误差均在0.3m以内,而BDS-3卫星均存在较长的连续观测历元的伪距多路径误差较大情况,基本在0.4m以上,表明BDS-2卫星的伪距多路径误差整体优于BDS-3,在BDS数据解算时,引入BDS-2卫星有利于提高解算精度。
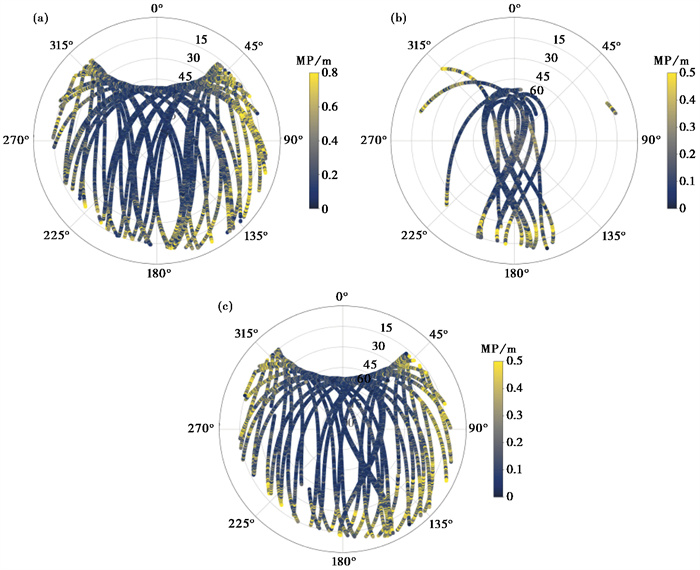
|
图 7 GPS(a)、BDS-2(b)、BDS-3(c)卫星的伪距多路径误差天空图 注:GPS卫星以L2为例,BDS-2卫星以B3I为例,BDS-3卫星以B3I为例。 |
综上,本文在初步BDS-3星座的基础上引入了BDS-2星座,并剔除了所有的GEO卫星,最终BDS星座的卫星可见数和四类DOP均与GPS相当,且BDS-2卫星观测数据质量整体优于BDS-3卫星,说明本文在数据处理时采用的BDS星座的合理性。对于BDS-3不同频点,B1C和B2a分别存在较小的信噪比和较大的伪距多路径误差,而B1I和B3I数据质量整体较优,加之两频点拥有更多的观测卫星,因此采用B1I和B2a频点进行高精度双差定位,有利于充分发挥BDS星座优势,提高数据解算精度。
3 精密星历精度分析为获得高精度的解算结果,除了筛选质量更优的观测数据,获取高精度的卫星轨道也至关重要。在GNSS高精度数据解算时,一般采用轨道精度最高的最终精密星历产品,目前仅有欧洲定轨中心(The Center for Orbit Determination in Europe,CODE)和武汉大学(Wuhan University,WHU)可以提供BDS-3的最终精密星历。
本文采用CODE和WHU提供的2021年DOY 068至2022年DOY 067共一年时间的BDS-3和GPS最终精密星历,基于GAMIT 10.71进行初始轨道积分拟合。采用的太阳光压模型为13参数ECOMC模型(Arnold et al,2015),地球反照模型为box-wing模型,天线推力模型为ANTBK模型。通过分析拟合结果的径向及三维均方根误差(3-Dimensional Root Mean Square,3D RMS)的均值,来评价精密星历的内符合精度。
对于MEO CAST卫星,CODE星历RMS优于WHU(图 8(a)),径向RMS在3mm左右,3D RMS在5.5mm左右;在WHU的数据中,C11、C12、C14三颗BDS-2卫星与CODE数据结果差异较小,其他卫星径向RMS在8.5~11.7mm之间,3D RMS在11.6~16.8mm之间。MEO SECM卫星间不存在显著差异(图 8(b)),其CODE数据RMS与MEO CAST卫星相当,而WHU数据RMS值小于MEO CAST卫星,这是由于两者航天器结构差异导致太阳光压建模精度略有差异,进而影响卫星轨道精度(Zhao et al,2022)。
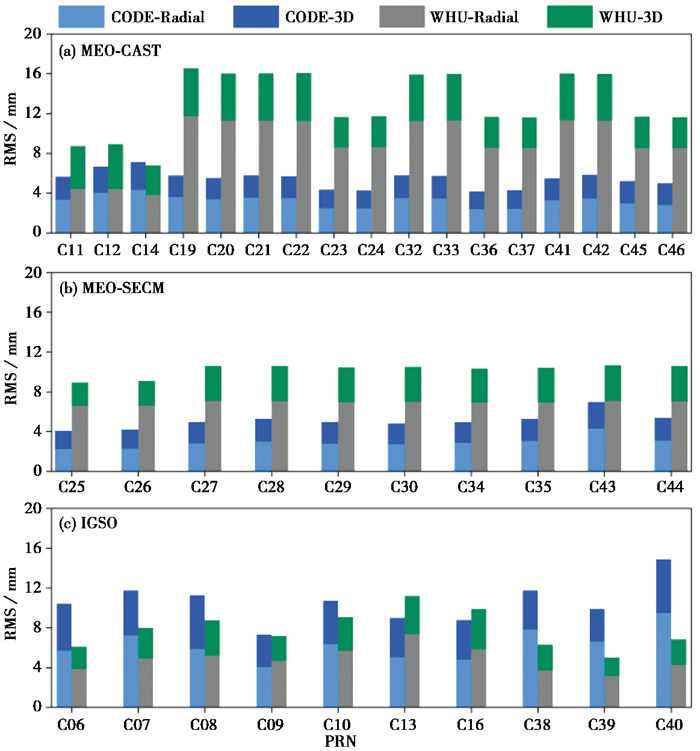
|
图 8 CODE和WHU提供的最终精密星历BDS-3不同卫星轨道拟合精度 |
对于IGSO卫星(图 8(c)),CODE数据径向RMS在4.7~9.5mm,3D RMS在7.3~14.9mm,WHU数据径向RMS在3.1~7.4mm,3D RMS在5~11.2mm,CODE数据RMS略大于WHU,且两者均大于MEO卫星的CODE数据,这可能是由于IGSO卫星的空间分布特征以及较高的轨道高度导致轨道径向精度较差。
整体而言,CODE数据所有MEO卫星轨道拟合精度差异性较小,径向RMS保持在4.5mm以内,3D RMS保持在8mm以内,明显优于WHU数据。而CODE数据IGSO卫星RMS大于WHU,但差异不大。因此,在BDS-3高精度数据解算中,为保证更高精度的轨道信息,应采用CODE提供的最终精密星历产品。
GPS卫星CODE数据和WHU数据的轨道拟合精度无系统性差异(图 9),径向RMS在3mm左右,3D RMS在5mm左右,与BDS-3 MEO卫星差异在±2mm以内,这表明GPS卫星轨道精度与CODE星历提供的BDS-3 MEO卫星轨道精度相当。但是,利用GAMIT10.71软件进行初始轨道拟合时,GPS采用了更为精细的非保守力建模,采用的太阳光压模型为ECOM模型,GPS能取得较高的精密定轨精度,但其无法精确描述BDS-3卫星的太阳光压摄动(Duan et al,2022)。此外,软件还无法对BDS-3卫星的地球反照辐射等精细化的非保守力进行建模,因此BDS-3卫星的轨道拟合精度有望进一步提高。
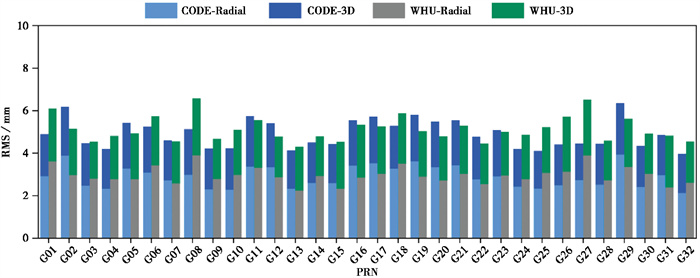
|
图 9 CODE和WHU提供的最终精密星历GPS卫星轨道拟合精度 |
在采用GAMIT进行高精度相对定位时,不同规模的观测网络需要制定不同的参考策略,以满足高精度解算需求。关键的参数配置直接影响基线解算精度,并通过协方差阵传递误差,间接影响最终测站点位精度。因此,本文针对以下关键参数配置进行实验分析:
(1) 基线解算模式。GAMIT提供了BASELINE和RELAX.两种模式用于基线解算(杨登科等,2016)。BAELINE模式固定了轨道和地球定向参数,RELAX.将轨道和地球定向参数作为待固定参数并设置了相应的先验约束。
(2) 观测值类型。观测值类型包括利用伪距求解宽巷模糊度的LC_AUTCLN解、添加电离层约束进行宽巷模糊度解算的LC_HELP解、分别采用L1/L2独立的双差观测组合的L1L2_INDEPENT解、仅采用L1、L2求解模糊度的L1_ONLY、L2_ONLY解(Herring et al,2015),由于新型接收机均可接收多频信号,故不考虑L1_ONLY、L2_ONLY解。
(3) 卫星截止高度角。在上文分析中,低高度角历元的数据质量较差,可能是由于天边卫星大气误差过大导致模糊度无法固定(罗权,2017)。但过大的卫星截止高度角可能使卫星可见数减少,星座几何强度弱,导致最终解算结果不理想。因此,选择适当的卫星截止高度角对于提高解算精度至关重要。
4.1 解算方案基于GAMIT10.71对大规模GNSS观测网进行基线处理时,不同规模的观测网络需要采用不同的解算策略,从而获取更高精度的解算结果。由于软件一般对短基线的解算精度较低,在解算前,采用间距分区法对观测网络进行分区,以减小短基线对处理精度的影响。
间距分区法(曹炳强等,2016)是对测站分布密集的测区进行分区的一种方法,该方法通过将布设比较密集的实验场测站抽稀,使相邻测站均匀分布在不同的测区,减少短基线数目,削弱了短基线对整体解算精度的影响,而且能有效提高解算效率。分区结果如 图 10所示。
|
图 10 利用间距分区法对测区进行分区结果 |
为探究基线解算模式、观测值类型和卫星截止高度角对基线解算结果的影响,获得最优的基线解算策略,本文选取实验场2022年DOY 001~030的观测数据,对不同研究因素分别选择不同的参数,其他参数保持一致,进行基线解算并评价解算精度。解算方案如 表 2所示,其他参数配置见 表 3。
| 表 2 解算方案设计 |
| 表 3 GAMIT基线解算策略 |
评价基线解算结果的好坏一般有以下3个评价标准:
(1) 标准化均方根误差NRMS(Normalized Root Mean Square)。用来描述单时段基线解算值偏离其加权平均值的程度(安向东等,2016),通常,NRMS值越小,意味着基线解算精度越高。一般认为NRMS不超过0.3说明解算成功(Herring et al,2015)。
(2) 基线重复性(慕仁海等,2020)。各时段解的基线重复性是衡量基线解算精度的重要指标,能反映基线解的内部精度。绝对基线重复性和相对基线重复性定义如下
| RL=√nn−1n∑i=1(Li−ˉL)2δ2in∑i=11δ2 | (1) |
| Rr=RLˉL | (2) |
其中,RL为基线L的绝对基线重复性;Rr为相对基线重复性;Li为第i天基线长,δi2为Li的中误差;Li为基线加权平均值,其公式如下
| ˉLi=n∑i=1L2i/δ2in∑i=11/δ2i | (3) |
(3) 基线分量解算精度。单时段基线解算后可获得每条基线E、N、U方向的解算精度,能够直观反映每条基线的解算精度的大小。
4.3 结果分析 4.3.1 基线解算模式分别采用BASELINE和RELAX.两种基线解算模式进行解算。RELAX.模式下的NRMS值略小于BASELINE,但两者差异不大,均保持在0.12~0.16之间(图 11(a)),符合GNSS高精度基线解算的要求。
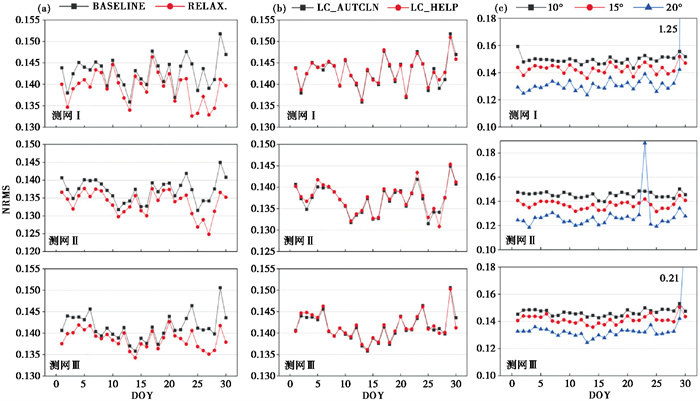
|
图 11 采用不同基线解算模式(a)、观测值类型(b)和卫星截止高度角(c)基线解算的NRMS值 |
实验场观测网络基线长度基本在400km以内,部分在400~600km,绝对基线重复性随基线长度的增大而增大。在200km以内,两种解算模式下的绝对基线重复性没有明显差异,均在6mm以内,大于200km时,RELAX.模式下的绝对基线重复性逐渐小于BASELINE模式,大于400km后RELAX.模式表现出明显的优势(图 12(a))。相对基线重复性如 图 12(b)所示,在200km以内,两种模式下的相对基线重复性均在3mm以上,在200km以后逐渐收敛,但两者无明显差异,400km以后RELAX.略优于BASELINE模式。
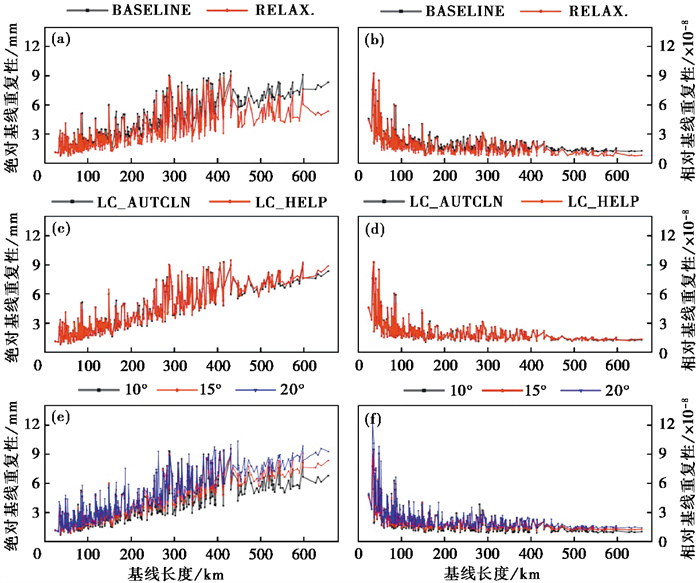
|
图 12 采用不同基线解算模式、观测值类型和卫星截止高度角时的绝对基线重复性(a)、(c)、(e)以及对应的相对基线重复性(b)、(d)、(f) |
采用不同解算策略时,对30天数据基线解算后在E、N、U方向的平均解算精度如 图 13所示。对于200km以内的基线,RELAX.模式下E、N方向上的解算精度略优于BASELINE,但差异较小,均在4mm以内;大于200km时,RELAX.仍保持较优的精度水平,而BASELINE解算精度逐渐变大,明显大于RELAX.(图 13(a))。在U方向上,基线长度对解算精度无明显影响,RELAX.下的解算精度整体略小于BASELINE。
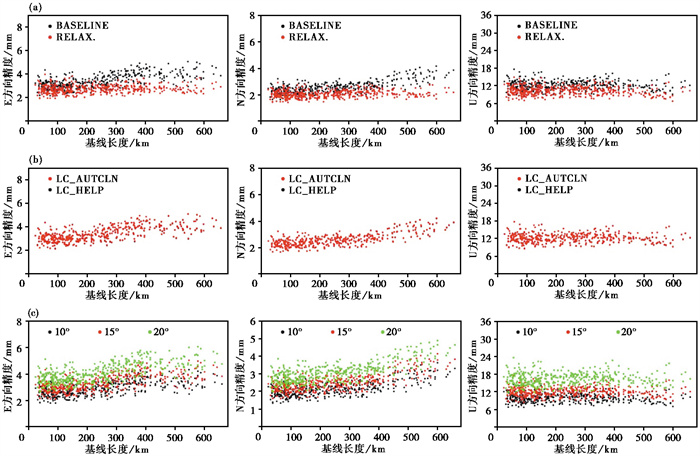
|
图 13 采用不同基线解算模式(a)、观测值类型(b)和卫星截止高度角(c)时基线在E、N、U方向上全部观测时段平均解算精度 |
综上分析,在基线长度大于200km时,RELAX.模式下的NRMS、基线重复性以及各基线分量解算精度均优于BASELINE,因此在密集观测网络的基线解算时,推荐采用RELAX.解算模式。
4.3.2 观测值类型实验表明,观测值类型采用L1, L2_INDEPEND.进行基线解算时,三个测区的NRMS全部大于0.5,无法成功进行基线解算。采用LC_AUTCLN和LC_HELP两种观测值类型,其NRMS值均在0.15内变化,符合解算要求,且两者大小相等,无明显差异(图 11(b))。
两者的绝对基线按重复性(图 12(c))和相对基线重复性(图 12(d))也基本一致,图 13(b)显示两种观测值类型在E、N、U方向的解算精度基本重合。结果表明,实验场北斗数据的伪距观测噪声水平很低,添加电离层约束对解算精度没有显著改善,因此在解算时推荐采用观测值类型为LC_AUTCLN。
4.3.3 卫星截止高度角采用不同卫星截止高度角解算时,NRMS差异较为明显(图 11(c)),大小关系如下:NRMS(20°)<NRMS(15°)<NRMS(10°)。三种方案NRMS均保持在0.12~0.16以内,但20°的个别解算结果NRMS值异常,甚至超过0.5,说明在20°时,一般可以获得很高的解算精度,但是同时由于剔除了大量观测数据,导致个别时段数据缺失,星座几何强度弱,最终导致基线解算精度变差。
由 图 12(e)可以看出,对于短基线而言,设置三种卫星截止高度角时,绝对基线重复性无明显差异,当基线长度大于300km时,三者显示出明显的大小关系:10°<15°<20°,且随着基线长度增大,差异也更加显著。由 图 12(f)可以看出,三者的相对基线重复性差异很小,其值在短基线时较大,200km后逐渐收敛,基线较长时表现出较小差异,大小关系与绝对基线重复性保持一致。
设置三种卫星截止高度角时,E、N、U方向上的解算精度随基线长度的变化趋势基本相同,其中20°时各分量的解算精度最大,15°次之,10°时最小(图 13(c))。因此,在基线解算时选择卫星截止高度角为10°左右为宜。
5 结论BDS-3的成功组网,使BDS在高精度数据解算与应用领域更具优势。本文利用中国地震科学实验场BDS观测数据,系统分析了星座定位性能、观测数据质量、精密星历精度以及不同解算参数设置4个因素对北斗高精度解算的影响,初步结论如下:
(1) 在剔除GEO卫星、保留BDS-2卫星后,实验场BDS-3观测数据的可见卫星数和四类DOP均保持在较优的水平,与GPS差异很小,且稳定性更强,不会对数据解算产生系统性影响;同时BDS-2卫星观测数据质量整体优于BDS-3卫星,说明了本文在数据处理时采用的BDS星座的合理性。
(2) BDS-3不同频点的信噪比均优于GPS,BDS-3新频点B1C信噪比表现不佳,B2a表现较优,且与B3I相接近;BDS-3的伪距多路径误差相对GPS较大,其中新频点B1C伪距多路径误差较小,与B1I相当,而B2a较大。为减少观测噪声和伪距多路径误差的影响,并充分利用BDS星座优势,在利用实验场北斗观测数据进行高精度数据解算时,推荐采用B1I和B3I频点进行高精度双差定位数据解算。
(3) 对于MEO卫星,CODE星历的轨道拟合结果明显优于WHU,径向RMS在3mm左右,3D RMS在5.5mm左右,与GPS结果差异在±2mm以内;而对于IGSO卫星,CODE数据轨道拟合精度不及WHU数据,但两者差异不大。因此,在BDS-3高精度数据解算时推荐采用CODE提供的最终精密星历。
(4) 通过对比分析不同解算参数下基线解算结果的NRMS、基线重复性以及基线各分量解算精度可以发现,基线解算模式选择RELAX.时,NRMS、基线重复性和基线各分量解算精度均优于BASELINE;观测值类型选择L1, L2_INDEPEND时不能成功解算基线,选择LC_AUTCLN和LC_HELP时NRMS和基线重复性无明显差异;设置卫星截止高度角为20°时存在NRMS值较大、甚至超限的情况,设置10°时基线重复性和各分量解算精度最小。因此,在实验场北斗观测数据高精度数据解算中,建议基线解算选择基线解算模式为RELAX.、观测值类型为LC_AUTCLN、卫星截止高度角为10°。
本研究可为北斗大规模区域网观测数据的高精度解算策略提供参考。同时,本研究表明,实验场北斗观测数据的定位性能、数据质量以及CODE提供的最终精密星历MEO卫星轨道拟合精度均与GPS相当,因此,BDS-3有望在高精度数据处理及地壳监测等领域得到更为广泛的应用。
安向东、杨登科, 2016, 测站间高差对短时段GPS基线解算的影响, 大地测量与地球动力学, 36(6): 534-538. |
曹炳强、成英燕、许长辉等, 2016, 间距分区法在解算卫星连续运行站数据中的应用, 测绘通报, (11): 15-17. |
柯晔, 吕志伟, 徐海龙, 等. 2021. BDS-3与GPS导航卫星星座性能对比分析. 见: 第十二届中国卫星导航年会论文集——S04卫星轨道与系统误差处理. 南昌: 31618部队, 31121部队.
|
李星星、张伟、袁勇强等, 2022, GNSS卫星精密定轨综述: 现状、挑战与机遇, 测绘学报, 51(7): 1271-1293. |
罗权, 2017, 不同截止高度角对GAMIT基线解算的影响分析, 测绘地理信息, 42(3): 14-17. |
吕春东、王佳、闫飞, 2018, 应用STK工具的BDS仿真分析, 导航定位学报, 6(2): 82-86. |
慕仁海、常春涛、党亚民等, 2020, GAMIT10.71解算GNSS长基线精度分析, 全球定位系统, 45(5): 14~19, 83. |
王敏、沈正康, 2020, 中国大陆现今构造变形: 三十年的GPS观测与研究, 中国地震, 36(4): 660-683. |
王西龙、许小龙、赵齐乐, 2023, 北斗三号系统信号质量分析及轨道精度验证, 武汉大学学报(信息科学版), 48(4): 611-619. |
王阅兵、甘卫军、陈为涛等, 2018, 北斗导航系统精密单点定位在地壳运动监测中的应用分析, 测绘学报, 47(1): 48-56. |
许扬胤、杨元喜、何海波等, 2018, 北斗全球卫星导航系统实验卫星测距信号质量分析, 武汉大学学报(信息科学版), 43(8): 1214-1221. |
杨登科、安向东、汤勰, 2016, GAMIT数据处理中基线解算模式的对比分析, 测绘地理信息, 41(2): 18-21. |
杨元喜、郭海荣、何海波等, 2021, 卫星导航定位原理, 北京: 国防工业出版社.
|
杨子辉、薛彬, 2022, 北斗卫星导航系统的发展历程及其发展趋势, 导航定位学报, 10(1): 1-14. |
张致伟、龙锋、赵小艳等, 2022, 川滇地区的震源机制解及应力场特征, 地震地质, 44(1): 170-187. |
赵大江、王斌、张涛等, 2023, 多系统基准站数据质量比较分析研究, 测绘科学, 48(9): 9-16. |
Arnold D, Meindl M, Beutler G, et al, 2015, CODE's new solar radiation pressure model for GNSS orbit determination, J Geodesy, 89(8): 775-791. DOI:10.1007/s00190-015-0814-4 |
Duan B B, Hugentobler U, Selmke I, et al, 2022, BeiDou satellite radiation force models for precise orbit determination and geodetic applications, IEEE Trans Aerosp Electron Syst, 58(4): 2823-2836. |
Herring T A, King R W, McClusky S C. 2015. GAMIT Reference Manual: GPS Analysis at MIT, Version 10.7. Cambridge: Massachusetts Institute of Technology.
|
Li X X, Yuan Y Q, Zhu Y T, et al, 2019, Precise orbit determination for BDS3 experimental satellites using iGMAS and MGEX tracking networks, J Geodesy, 93(1): 103-117. |
Su X N, Meng G J, Sun H L, et al, 2018, Positioning performance of BDS observation of the crustal movement observation network of China and its potential application on crustal deformation, Sensors, 18(10): 3353. |
Wang F, Wang M, Wang Y Z, et al, 2015, Earthquake potential of the Sichuan-Yunnan region, western China, J Asian Earth Sci, 107: 232-243. |
Yang Y X, Gao W G, Guo S R, et al, 2019, Introduction to BeiDou-3 navigation satellite system, Navigation, 66(1): 7-18. |
Zhao Q L, Guo J, Wang C, et al, 2022, Precise orbit determination for BDS satellites, Satel Navigat, 3(1): 2. |
 2024, Vol. 40
2024, Vol. 40



