0 引言

固体地球潮汐形变简称固体潮，是固体地球对天体(主要是月亮和太阳)起潮力的一种响应。固体地球在日、月起潮力的作用下，地面会发生周期性的形变，局部产生倾斜。固体潮实测振幅与理论振幅的比值称为潮汐因子，潮汐因子是反映地球弹性力学性质的物理量，其实质是固体潮实测振幅与理论振幅的比值，分析潮汐因子的变化可表征观测点弹性模量的变化，从而推断观测点状态的变化(张晶等，2003)。

初步推断2023年8月6日山东平原5.5级地震发震断层为林南断裂(张雅茜等，2023)。该断裂延伸长度约25km，自西向东走向具有NEE向、近EW向至NEE向变化的趋势，断裂南倾，表现为高角度铲式正断层。震源机制解显示平原地震为一次走滑型为主的事件，矩震级为M_W5.5，矩心深度11km，断层节面Ⅰ的走向、倾角和滑动角分别为123°、62°、-24°，断层节面Ⅱ的走向、倾角和滑动角分别为225°、80°、-150°。截至2023年8月7日12时，山东平原5.5级地震序列共记录到余震87个，其中最大余震为8月6日3时2分发生的3.0级地震，余震主要集中分布在主震北东侧10km范围内，大致呈NEE向分布。

2023年8月6日山东平原5.5级地震后，中国地震台网中心梳理了震前震中距200km内地球物理台站数据异常情况，发现仅河北省兴济台地电阻率NE向自2022年4月1日开始出现电阻率数据偏离年变的下降变化，由于不同学科数据异常产生机理不同，本文仅对形变学科数据进行讨论。中强地震前地球物理数据是否存在潜在异常情况值得进一步分析和研究。

利用潮汐参数进行地震预测预报工作由来已久，学者们多致力于研究潮汐地震的触发作用，利用形变观测资料探讨固体潮与地震关系的研究较多(Tanaka et al，2004；Bouasla，2009；吴翼麟等，1993；薄万举等，1996；何翔，1996；黎凯武，1998；沈旭章等，2004)，而利用形变固体潮动态组合特征量来进行的研究则甚少。

本文在分析2023年8月6日平原地震前震源周边10个台站地倾斜潮汐因子时空变化特征的基础上，将EW和NS两分量的固体潮潮汐因子进行动态组合分析，进一步研究动态组合特征量与该地震的关系，研究结果对进一步分析平原地震前地球物理数据异常有一定的参考意义。

1 资料选取

本文选取平原周边观测质量较好、固体潮清晰的10个地倾斜台站作为研究对象，台站具体分布情况见 图 1，台站信息见 表 1。为反映真实倾斜固体潮特征，收集各台站2020年1月1日—2023年11月31日地倾斜整点值数据，删除错误数据后采用克里金差值法(董博等，2016)对数据进行差值补全。利用EIS2000处理软件(蒋俊等，2000)中维尼迪可夫(Venedikov)调和分析方法对所选观测资料EW和NS向数据进行计算。

2 地震过程中天体引潮力附加构造应力变化

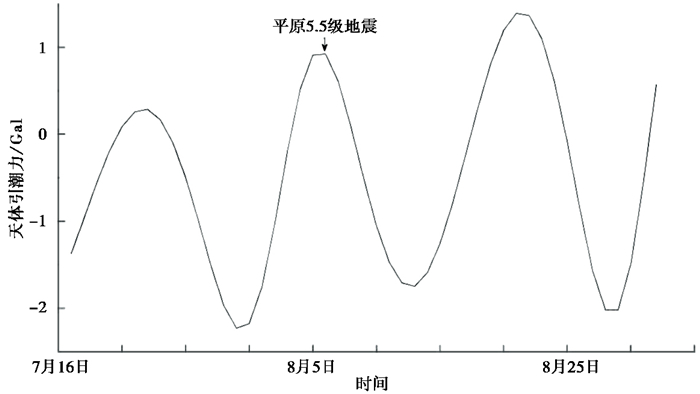
Heaton(1975)研究表明，引潮力是持续周期性变化的，其在最大振幅相位时刻，有可能诱发地应力处于临界状态的构造区发生地震。对于平原5.5级地震，利用已有的潮汐计算方法(Zhang et al，2018)，计算2023年7月16日—8月31日震中位置的引潮力连续变化值，结果如 图 2所示。

由 图 2可知，引潮力处于高相位值时平原5.5级地震发生(箭头所指位置)，认为引潮力对该次地震有一定的诱发作用。本次地震发生在引潮力极大值的转折点(8月5日、8月6日)，引潮力处于临界状态，表明平原地震的发生与天体间引潮力瞬时变化有一定关系，且震前应力变化应该是逐渐积累、增强的过程。

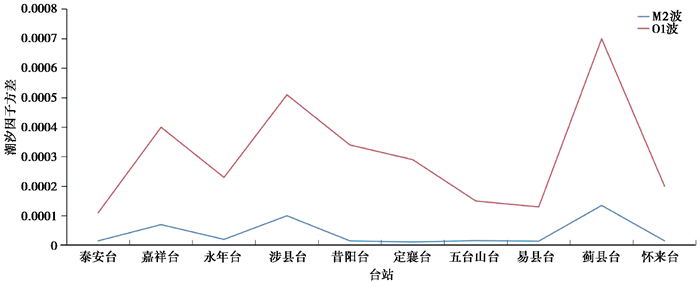
3 稳定性分析 3.1 O1波与M2波稳定性分析

计算10个台站每月M2波、O1波潮汐因子，得出其方差变化曲线，如 图 3所示。由图可知，O1波的潮汐因子方差要明显比M2波潮汐因子方差大。2020年1月1日—2023年11月31日，O1波方差基本维持在0.5‰以内(涉县台、蓟县台除外)；而除蓟县台外，其余9个台站M2波方差基本维持在0.1‰以内。由此可看出M2波稳定性要好于O1波，故本文分析采用地倾斜M2波潮汐参数。

3.2 地倾斜EW向与NS向潮汐因子稳定性分析

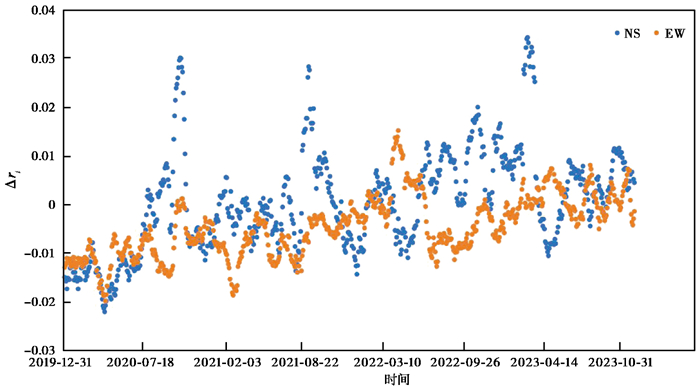
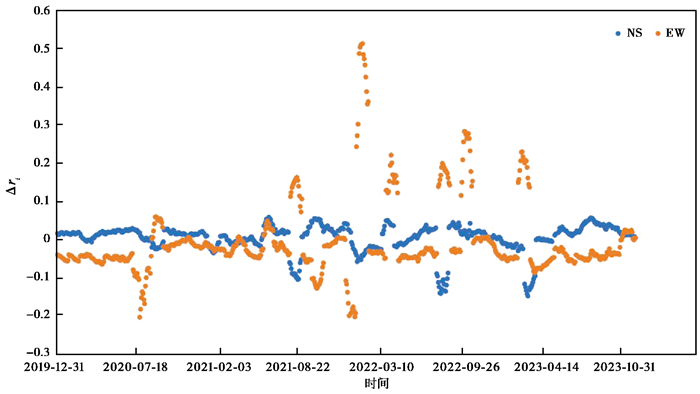
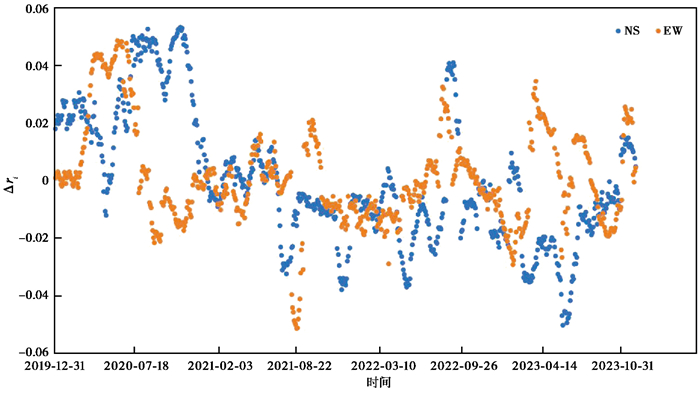
利用Venedikov调和分析方法对10个地倾斜观测站的观测资料进行分析，获取倾斜固体潮M2潮汐因子变化曲线。计算各台站潮汐因子Δr_i异常的公式为：Δr_i=r_i-r，其中，r_i为第i月的潮汐因子值，r为潮汐因子的平均值(傅再扬等，2007)。根据上述公式计算平原地震邻区10个台站地倾斜固体潮EW向和NS向潮汐因子，比较两个方向潮汐因子的差异性，分析认为大部分台站(泰安台、永年台、涉县台、昔阳台、易县台、蓟县台、怀来台)EW向潮汐因子变化相对稳定，NS向表现的较为离散，以蓟县台为例进行说明，见 图 4；嘉祥台和定襄台潮汐因子表现相反，NS向相对较稳定而EW向表现较为离散，以定襄台为例进行说明，见 图 5；五台山台EW向和NS向潮汐因子离散程度相差不大，见 图 6。总体可以看出，泰安台、永年台、涉县台、昔阳台、易县台、蓟县台、怀来台EW向潮汐因子相对稳定，而嘉祥台和定襄台NS向潮汐因子相对稳定，五台山台EW向和NS向潮汐因子稳定性相差不大。基于EW向和NS向潮汐因子稳定性，后续分析中泰安台、永年台、涉县台、昔阳台、易县台、蓟县台、怀来台采用EW向潮汐因子，嘉祥台和定襄台采用NS向潮汐因子，五台山台、蓟县台等台站采用EW向潮汐因子。

4 潮汐因子时空变化特征分析 4.1 潮汐因子时间变化特征

潮汐因子等固体潮参数的时间序列变化可反映观测点周边地壳介质物性的变化。当孕震介质性质发生变化进入非弹性阶段时可能会出现潮汐因子中短期异常，这为地震前兆异常的分析判别提供重要信息。

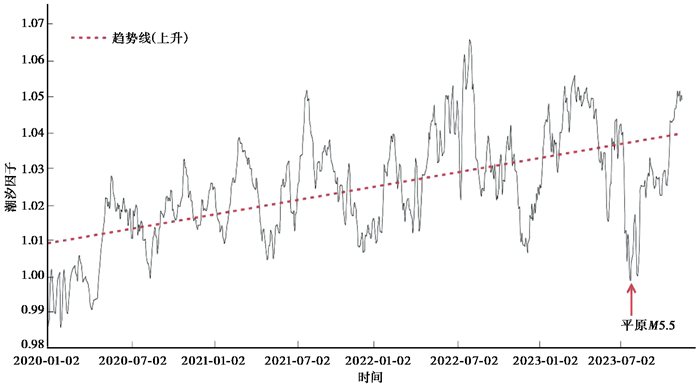
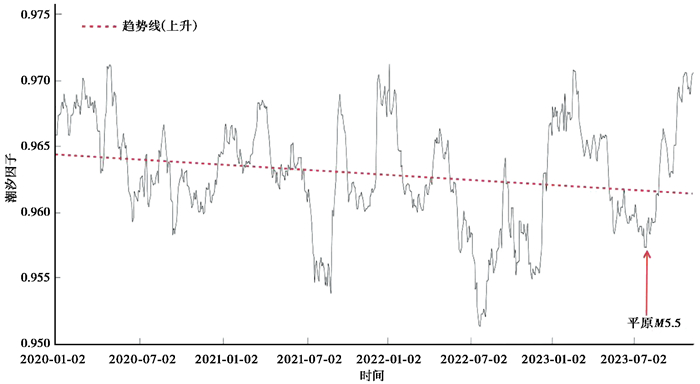
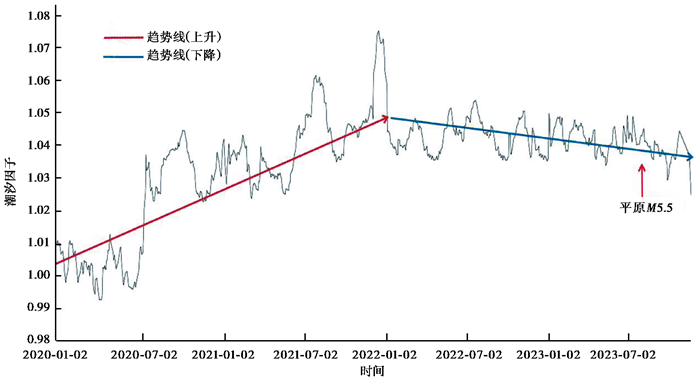
根据各台潮汐因子曲线变化形态，大致可分为三组：①趋势以上升为主，以永年台为例，如 图 7；②趋势以下降为主，以怀来台为例，见 图 8；③趋势先上升后下降，以泰安台为例，见 图 9。

根据计算结果可知，2023年8月6日平原5.5级地震前，有5个地倾斜台站潮汐因子处于趋势性上升，分别为永年台、涉县台、五台山台、定襄台、昔阳台。2020年1月—2023年11月永年台潮汐因子从0.99上升至1.05，上升速率较快。8月6日平原地震前永年台潮汐因子未出现震前异常，基本在0.9987左右浮动。从 图 7可知，永年台潮汐因子大致存在一个4个月的变化周期，通常以阶变的形式结束一个周期变化。潮汐因子增大表明该区域弹性特征增强，表现为应力积累。

涉县台潮汐因子基本在0.61~0.63区间波动，2023年2月3日涉县台潮汐因子出现大幅阶变，从0.6132上升至3月7日的0.65，至4月14日又下降至0.6192，后基本维持在0.62左右。五台山台潮汐因子基本维持在0.47左右，2023年2月19日潮汐因子从0.4821急剧下降至3月17日的0.3109，后急剧增大至4月22日的0.4755，后变化较稳定，阶变幅度约为53%。2023年2月5日昔阳台潮汐因子从1.0851急剧上升，至3月3日达到极大值1.3666，后开始回落，4月17日下降至1.0907后基本达到稳定。定襄台潮汐因子与五台山台变化情况类似，2023年2月19日潮汐因子从1.4936快速下降至3月7日的极小值1.3634，后又快速上升至4月10的1.5098。潮汐因子波动不大，表明该区弹性特征变化不明显。

震前有2个台站潮汐因子处于下降趋势，为怀来台和蓟县台。怀来台潮汐因子大致存在1年的变化周期，每年7月底至8月中旬潮汐因子达到极小值后开始上升，潮汐因子整体处于逐渐下降状态，震前潮汐因子未出现异常。2023年2月5日蓟县台潮汐因子从0.7083迅速上升至2月17日的0.7343，达到极大值后急剧下降，4月14日达到极小值0.691，后续基本在0.70左右小幅波动。潮汐因子减小表明该区域弹性特征减弱，表现为应力减弱。

震前有3个台站潮汐因子处于先上升后下降趋势，分别为泰安台、易县台和嘉祥台。三个台站潮汐因子变化趋势较为一致，2020年至2022年上半年表现为上升趋势，2022年年中至2023年底表现为下降趋势。泰安台潮汐因子基本在1.03~1.05左右变化，2020年1月1日—2022年1月18日前潮汐因子处于上升趋势，2022年至2023年底潮汐因子基本处于下降趋势，潮汐因子变化趋势在2022年初发生转折。震前易县台潮汐因子也出现了阶变变化，从2023年2月5日的0.6446急剧下降为2月17日的0.5282，之后迅速回升至3月14日的0.6685。震前嘉祥台潮汐因子未表现出明显异常。潮汐因子先趋势性增大后趋势性减小，可能与台站应力积累有关，震前震中附近应力积累，表现为潮汐因子增大，一定程度后，受震前闭锁剪力影响，应力减弱，潮汐因子开始下降。

2023年2月初，震中东部五台山台、定襄台、昔阳台、涉县台4个台站和北部的易县台、蓟县台潮汐因子均发生大幅度阶变，4月中下旬阶变基本结束。而同样位于震中北部的怀来台其潮汐因子在震前却未表现出异常变化，这可能与震中距较大有关，震中东部的永年台潮汐因子也未出现异常变化，这可能与台站周边地质构造有关。

4.2 潮汐因子空间变化特征

为了更清晰地观察潮汐因子变化特征，更深入地分析潮汐因子的变化规律，绘制了10个台站地倾斜潮汐因子长趋势变化空间分布图，见 图 10。

由 图 10可知，震前2年，北部震中距372km的怀来台和震中距339km蓟县台潮汐因子处于下降趋势，其余台站潮汐因子均处于上升趋势。

震前1年，震中南部的嘉祥台、泰安台，北部怀来台、蓟县台和易县台潮汐因子均表现为下降趋势，而震中西部的五台山台、定襄台、昔阳台、涉县台和永年台潮汐因子则均表现为上升趋势，虽震中东部无地倾斜台站，但仍能清晰地看出震中SN向潮汐因子呈现出下降的状态，而EW向则为上升状态。

震前2年，震中北部的易县台(震中距257km)、震中南部的嘉祥台(震中距192km)和泰安台(震中距126km)潮汐因子均表现为上升趋势，根据历史震例总结，大震前震源附近震中距300km的范围内会有应力积累过程(黄雅等，2020)。而震前1年三个台站潮汐因子变化趋势发生转折，均表现为下降趋势，两个时间尺度的变化趋势发生转折。潮汐因子的变化反映了地壳弹性特征的变化，潮汐因子变化增大表明实际观测的潮波振幅比平均潮波振幅要大，该区域弹性特征增强，反之，则弹性特征减弱。根据平原地震震源机制解可知，本次地震最大主压应力为近EW向，而近SN向表现为拉张应力。图 10研究结果符合本次地震震源机制解，震前潮汐因子上升和下降的趋势变化大体呈四象限分布，平原地震震中位于四象限对称中心附近，这种特征可用震前闭锁剪力模型来解释(郝洪涛等，2015)。

5 潮汐因子动态组合 5.1 潮汐因子动态组合方法分析

将地倾斜固体潮EW和SN两个方向的潮汐因子进行组合，组合后的物理量可以更好地解释介质所处状态，并且能较好地阐明岩石破裂前的某些特征，避免了采用单一方向时的局限性，使分析结果更加真实可靠。

吴翼麟等(1993)提出倾斜固体潮振幅因子动态组合概念，其中Δr有如下特征量：

(1) 取用Δr_EW值，则Δr_EW=r_EW-r_EW；

(2) 取用(Δr_EW+Δr_NS)值，则(Δr_EW+Δr_NS)=(r_EW-r_EW)+(r_NS-r_NS)。物理上可解释为该处介质扩容引起的膨胀；

(3) 取用(Δr_EW-Δr_NS)，物理意义上可解释为该处介质的剪切应变；

(4) 取用(Δr_EW/Δr_NS)，物理意义上可解释为振幅因子异常的各向异性，一般是介质中具有众多定向微破裂时特征。

本文绘制了10个台站地倾斜潮汐因子动态组合的3种特征量进行分析，根据计算结果可知，震前10个地倾斜台潮汐因子动态组合特征量均出现异常变化，变化曲线见 图 11。

根据 图 11可知，平原5.5级地震震前测区介质扩容引起的膨胀(Δr_EW+Δr_NS)和剪切应变(Δr_EW-Δr_NS)表现出快速上升或下降的变化。(Δr_EW+Δr_NS)和(Δr_EW-Δr_NS)出现阶变的时间较统一，主要集中在2023年1月底至3月底，其中，定襄台为2月7日—3月23日，怀来台为2月5日，蓟县台为2月7日—3月17日，涉县台为2月15日—3月29日，泰安台为1月4日—2月7日，五台山台为1月24日—3月3日，易县台为1月20日—2月19日，嘉祥台为1月20日—2月11日，昔阳台为1月28日—4月27日。永年台(Δr_EW+Δr_NS)和(Δr_EW-Δr_NS)异常出现时间稍晚于其他台站，为临震前的6月14日—7月28日。

除永年台外，大部分台站潮汐因子异常的各向异性(Δr_EW/Δr_NS)发生大幅变化的时间稍晚于介质扩容引起的膨胀(Δr_EW+Δr_NS)和剪切应变(Δr_EW-Δr_NS)发生异常的时间，(Δr_EW/Δr_NS)异常主要集中在4月至5月。

5.2 潮汐因子时空特征与动态组合特征量分析

总结地倾斜台站潮汐因子变化规律和潮汐因子动态组合特征量变化规律，结果见 表 2。结合上述分析可知：

(1) 五台山台、定襄台、涉县台、蓟县、昔阳和易县台6个台站2023年1—3月介质扩容引起的膨胀(Δr_EW+Δr_NS)和剪切应变(Δr_EW-Δr_NS)出现异常变化，潮汐因子2月至4月发生异常变化，而潮汐因子各向异性(Δr_EW/Δr_NS)主要集中在5月前后。

震前(Δr_EW+Δr_NS)出现大幅度异常，表示岩石介质的扩容膨胀；(Δr_EW-Δr_NS)阶变，表示岩石介质的切向应变，可以清楚地显示出地震的发展过程，(Δr_EW/Δr_NS)变化剧烈，表示岩石介质的各向异性有明显异常。这说明震前区域应力调整首先引起测区介质受力状态发生改变，即介质扩容膨胀或者切向应变变化，进而使得该区弹性特征改变，引起潮汐因子振幅发生异常，最后表现为振幅因子异常的各向异性出现异常，介质中具有众多定向微破裂，继而发震。

(2) 震前永年台、怀来台、泰安台和嘉祥台潮汐因子未表现出异常变化，而潮汐因子组合动态特征量却出现明显的异常变化，这说明潮汐因子动态组合方法相较潮汐因子原始曲线法，能够提取到更丰富的异常信息。

6 结论与讨论

本文通过分析山东平原地震周边10个地倾斜台站潮汐因子2020年1月—2023年11月的时空变化特征和潮汐因子动态组合特征，得到如下认识：

(1) 天体间引潮力瞬时变化对平原地震的发生有一定的诱发作用，且震前应力应该是逐渐积累、增强的过程。

(2) 受本次地震主应力方向影响，M2波潮汐因子的上升与下降变化趋势大体呈四象限分布，平原地震震中位于四象限对称中心附近。

(3) 潮汐因子组合特征量与平原地震的发生有较好的对应，可以看出，震前(Δr_EW+Δr_NS)出现明显的异常，表征岩石介质的扩容膨胀；(Δr_EW-Δr_NS)阶变，表征岩石介质的切向应变，可以清楚地显示出地震的发展过程，(Δr_EW/Δr_NS)变化剧烈，表示岩石介质的各向异性有明显异常。

上述结论说明震前区域应力调整首先引起测区介质受力状态发生改变，进而使得该区弹性特征改变，引起潮汐因子振幅发生异常，最后表现为振幅因子异常的各向异性出现异常，介质中具有众多定向微破裂，继而发震。

分析地倾斜固体潮潮汐因子特征量动态组合变化，可作为探测孕震区岩石状态变化的一种方法，可以监测中强地震孕育过程中振幅因子异常的时空变迁特点，其结果的物理解释与室内岩石的破裂实验相似。

致谢: 感谢审稿专家对本文提出的宝贵修改意见。